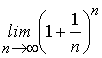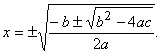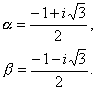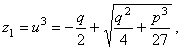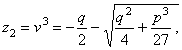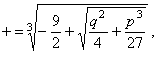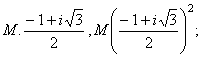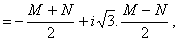| E | Sexta letra del abecedario de mayúsculas que suele emplearse para indicar la parte entera de un número, el cual se escribe entre paréntesis, así: E(n).- | ||||||||||||||
| e |
Sexta
letra del abecedario de minúsculas y segunda de las vocales castellanas.
Se emplea para designar la
base de los logaritmos naturales, número cuya irracionalidad estableció
Euler en 1748, y posteriormente, en 1873, Hermite consiguió demostrar que
era trascendente. Este famoso número está
definido por la expresión:
|
||||||||||||||
| e | Épsilon, quinta letra del alfabeto griego de minúsculas, que se emplea generalmente para representar números muy pequeños o infinitésimos , también simboliza el error .- | ||||||||||||||
| éctasis | Del griego ecqesiz. Repetición del enunciadode un problema referido a un caso particular. | ||||||||||||||
| ecuación | Igualdad
que involucra valores desconocidos llamados “incógnitas” y se
convierte en una identidad cuando en vez de las incógnitas, se reemplazan
por ciertos valores, diciendose entonces que la ecuación se verifica o
se satisface para tales valores, y en esto se diferencia,
precisamente de la igualdad, que se verifica o satisface para todos los
valores de sus letras. Por ejemplo la expresión: ( a+b). (a - b) = a2
- b2
, es una igualdad que se verifica para cualquier par de valores a y
b y se traduce al lenguaje cotidiano diciendo: "El producto de la
suma de dos números cualesquiera por su diferencia es igual a la
diferencia de los cuadrados de dichos números", que conforma un
teorema. Mientras que la expresión: 7.a = 14, es una ecuación y solo se
satisface para a=2.
Las letras que se deben sustituir para que la ecuación se convierta en identidad ( ejemplo: 7 . 2 = 14), se denominan incógnitas; y los valores de las incógnitas que satisfacen una ecuación reciben el nombre de raíces o soluciones de la ecuación, y el procedimiento que debemos seguir para hallar las raíces o soluciones de la ecuación, se denomina resolución de la ecuación. Los procedimientos que existen para resolver ecuaciones son variados y dependen del tipo de ecuaciones a resolver.- |
||||||||||||||
| ecuación abeliana | Nombre dado en honor a Abel, a la ecuación del tipo: f(x)=0, si todas sus raíces o soluciones son funciones racionales de una de ellas y tales que siendo xr=jr(x0); xs=js(x1); tal que sea jr .js=js.jr | ||||||||||||||
| ecuación algebraica | Es aquella cuyo primer miembro es
una función algebraica de la incógnita o incógnitas que la constituyen.
Toda ecuación algebraica de una sola incógnita o de una sola variable, una vez quitados los denominadores y radicales y hecha la transposición de términos, se puede siempre reducir a una expresión algebraica racional y entera de la
en la cual los coeficientes
La resolución de las ecuaciones algebraicas se funda en los siguientes teoremas: I. Si dos números sustituídos en vez de x en la función continua f(x) dan resultados de signos contrarios, la ecuación f(x) = 0 tiene, a lo menos, una raíz real comprendida entre los dos números sustituídos, y, en general, un número impar de raíces, y recíprocamente. II. Si dos números sustituidos en vez de x en la función continua f(x) dan resultados del mismo signo, la ecuación f(x) = 0 no tiene ninguna raíz real comprendida entre los dos números sustituídos o tiene un número par de ellas. a) Una ecuación cuyos términos sean del mismo signo, no puede tener raíces positivas reales. b) Todas las raíces reales de una ecuación completa de signos alternativamente positivos y negativos, son positivas. III. Una ecuación algebraica de coeficientes reales y de grado impar tiene, a lo menos, una raíz real de signo contrario al de su último término y, en general, un número impar. IV. Toda ecuación algebraica de coeficientes reales y de grado par cuyo último término es negativo, tiene a lo menos dos raíces reales, una positiva y una negativa, y, en general, un número impar de cada clase.
|
||||||||||||||
| ecuación absurda | La que no tiene solución. | ||||||||||||||
| ecuación bicuadrada | Véase Ecuación bicuadrática. | ||||||||||||||
| ecuación bicuadrática | La
de cuarto grado sin potencias impares de la incógnita. Se reduce,
pues, a la forma
y poniendo
y, por consiguiente,
resulta la ecuación
de segundo grado en
cuyas raíces son
luego las de la ecuación dada son:
La ecuación bicuadratica tiene, por tanto cuatro raices. Si es b2 -4ac < 0, los valores de y son imaginarios y, por tanto, los de x. Si es b2 -4ac = 0, los valores de x son dos a dos iguales y reales si a y b tienen signos opuestos. Si es b2 - 4ac > 0, los valores de y son reales. Si son positivos, las cuatro raíces de la ecuacion biuadratica son reales; si uno es positivo y otro negativo, los de x son dos reales y dos imaginarios, y si los dos valores de y son negativos los cuatro de x son imaginarios. El detalle queda consignado en el cuadro siguiente:
|
||||||||||||||
| ecuación binomia. | Toda
ecuación que se puede poner bajo la forma
xm - A = 0. [1] Si es a la raíz m-sima aritmética de A e y la expresión por la cual hay que multiplicar a para determinar los m valores de x, tendremos
y como a es una raíz de la ecuación [1], es
de donde, dividiendo por
y, por tanto:
lo que nos dice: Para encontrar los valores de x que satisfacen la ecuación [1] basta multiplicar la raíz m-sima aritmética de a por las m raíces m-simas de la unidad; luego la resolución de la ecuación binomia general [1] queda reducida a la de la ecuación
y por ser
|
||||||||||||||
| ecuación cíclica | Ecuación irreducible cuyas raíces están
ligadas por una función racional j
en orden circular :
|
||||||||||||||
| ecuación consecuencia de otras | La que se deduce de ellas por medio de una combinación lineal, y, por tanto, si forma parte de un sistema, se puede suprimir porque las soluciones del sistema que resulte de tal supresión son las mismas que las del primitivo, propiedad que se expresa diciendo que ambos sistemas son equivalentes. | ||||||||||||||
| ecuación cuadrática | Véase Ecuación de segundo grado. | ||||||||||||||
| ecuación cuártica | La ecuación general de cuarto grado, después
de dividirla por el primer coeficiente, es f (x) = x4 +A1 x3 +A2x2 + A3x+A4= 0. [1] Para transformarla en otra que carezca del término en x3 pondremos x = y-a1/4 puesto que es f '''(x) = 24x +6a1, dándonos dicha sustitución x4 + px2 + qx + r = 0, [2] y haciendo en ésta x = u + v + w, se tiene: x4 - 2 (u2
+ v2 + w2) x2 + 8uvw + [(u2 +
v2 + w2)2 -4 (u2 v2
+ v2 w2 + w2 u2 )] = 0,
y disponiendo de las indeterminadas u, v y w de modo que sea u2
+ v2 + w2 = -
uvw
=
u2
+ v2 + w2 = - que resultan conservando la primera de las anteriores y poniendo en la tercera (u2 v2 w2)2 = p2 |
||||||||||||||
| ecuación cúbica | Antes de estudiar la ecuación general de tercer
grado consideremos los dos casos particulares siguientes:
I. Si la ecuación es x3 - 1 = 0, (1) es evidente que una de sus tres raíces es 1, y, por lo tanto, el primer miembro de (1) es divisible por x - 1, siendo las otras dos raíces las de la ecuación de segundo grado x2 + x + 1 = 0 (2) que resulta de dividir el primer miembro de la (1), o sea, las tres raíces cúbicas de la unidad, son: x = 1,
Véase raíz de un número complejo. II. Si la ecuación es x3 - A = 0, (3) se tendrá:
x =
y si es la raíz cúbica aritmética de A y b la expresión por la cual hay que multiplicar a para tener las tres raíces de la ecuación dada, es
y elevando al cubo: a3 = A , a3 b3 = A, de donde:
b3 = 1 ; b =
lo que nos dice: Las raíces de la ecuación (3) se obtienen multiplicando la raíz cúbica aritmética de A por las tres raíces cúbicas de la unidad; pero como estas tres raíces están ligadas por las relaciones
1 +
como
fácilmente se comprueba sustituyendo en ellas los valores de
III. Consideremos ahora el caso general. Toda ecuación cúbica completa se puede escribir bajo la forma A0x3 + A1 x2 + A2 x + A3 = 0, (5) la cual se transforma en x3 + px + q = 0 (6) aplicando a la (5) las reglas de transformación de ecuaciones. Para resolver esta transformada (6), sean (u) y (v) dos arbitrarias y pongamos x = u + v. (7) Elevando al cubo, es x3 = u3 + 3u2v + 3uv2 + v3 = 3uv (u + v) + u3 + v3 de donde: x3 - 3uvx - (u3 + v3) = 0, (8) Ahora bien; puesto que u y v son arbitrarias, dispongamos de ellas de modo que sea 3uv = - p , u3 + v3 = q, (9) y entonces las ecuaciones (6) se verificará para x = u + v. Elevando al cubo la primera de las igualdades (9) es 27u3 v3 = -p3 (10) expresión que, con la segunda de las (9), nos dice que u3 y v3 son las raíces de una ecuación de segundo grado cuyo segundo coeficiente es q y el término independiente
de donde:
y de aquí:
y en virtud de (7)
que es la llamada fórmula de Cardano por haberla publicado éste en su Ars Magna, Nuremberg, 1545, pero que, en realidad, el primero que la encontró fue Tartaglia. Cada uno de los radicales (12) tiene tres valores que, combinados en la fórmula (13), dan nueve valores para x, pero como la ecuación (6) sólo tiene tres raíces, se han introducido seis raíces extrañas, y, por consiguiente, hay que combinar pares de valores de u y v de modo que sea 3uv = - p . Si es M un valor del primer radical (12) y N uno del segundo, los otros valores del primer radical serán
y los del segundo
y las tres raíces de la ecuación propuesta: x1= M + N ,
x2 =
x3
puesto que, por hipótesis, ha de ser
y siendo
el producto de las raíces aritméticas que hay que asociar para tener los valores de x debe ser igual a
o a MN. Al ser reales los coeficientes p y q de la ecuación (6), hay que tomar los de u y v de modo que el producto uv sea real, y, es esta hipótesis, distinguiremos tres casos, según que
sea positivo, nulo o negativo. a)
En el primer caso, los radicandos de la fórmula (13) son reales y
desiguales y cada uno de los radicales tiene un valor real y dos
imaginarios, siendo distintos los de uno y otro radical, y como el
producto de estos valores reales es
x1 = M + N,
lo que nos dice: La ecuación tiene una raíz real y dos imaginarias conjugadas. b)
Si es
los
valores de M y N son iguales y las raíces de la ecuación
serán
es decir: La ecuación tiene reales sus tres raíces, siendo dos de ellas iguales entre si, c)
Si es
los radicandos de la fórmula (3) son imaginarios conjugados, y, por consiguiente, los valores de los radicales; de modo que si es a + bi uno de los valores del primer radical, los otros dos son: (a + bi) a , (a + bi) a2 , donde a es una de las raíces imaginarias de la unidad, y los valores del segundo radical serán:
poniendo en las fórmulas (14) M = a + bi , N = a - bi , las raíces de la ecuación
son reales. La
primera de estas raíces no puede ser igual a ninguna de las otras dos,
porque si fuera de donde: a + bi = a (1± 3i) = - 2 aa, y elevando al cubo:
igualdad absurda porque, siendo, por hipótesis
el cubo de a + bi no puede ser igual a un número real - 8a3, como las dos últimas raíces tampoco pueden ser iguales por ser b ¹ 0, resulta: Las tres raíces de la ecuación son reales y desiguales. Este caso presenta notables particularidades. La fórmula (13) expresa las raíces mediante radicales de radicandos complejos, de modo que dando a éstos la forma a + bi y a - bi , las tres raíces de la ecuación (6), son como acabamos de ver:
x1 = 2a ,
x2 = -a + b
x3 = -a - b
|
||||||||||||||
| ecuación de Ampere | |||||||||||||||
| ecuación de d'Alembert | Véase cuerda vibrante | ||||||||||||||
| ecuación de Bernoulli | |||||||||||||||
| ecuación de Bessel | |||||||||||||||
| ecuación de Boyle-Mariotte | |||||||||||||||
| ecuación de congruencia | |||||||||||||||
| ecuación de Chebycheff | |||||||||||||||
| ecuación de Euler | |||||||||||||||
| ecuación de Fermat | |||||||||||||||
| espacio de N dimensiones | Un espacio es de n
dimensiones, cuando para determinar cada uno de sus puntos hacen falta los
valores de n parámetros llamados Coordenadas del Punto y que se
representan por X1, X2, ..... Xn |
||||||||||||||
| espacio afin | Espacio AFIN de n dimensiones es el espacio entre cuyos puntos y los conjuntos de n números reales cualesquiera X1, X2, ..... Xn llamados coordenadas del punto, se puede establecer una correspondencia biunívoca. | ||||||||||||||
| espacio métrico |
Es un Espacio AFIN en el cual se introduce la manera de medir la distancia entre dos puntos cualesquiera del mismo. |
||||||||||||||
| espacio euclidiano |
Un Espacio es EUCLIDIANO y de dimensión n cuando : 1.- Es AFIN de dimensión n 2.- La distancia entre dos puntos cualesquiera del mismo está definida por :
Llamando d (A,B) a la distancia entre los puntos A y B del E2 se verifica que : 1)
d (A,B) = 0 Û A = B 2)
d (A,B) = d (B,A) 3) d (A,C) + d (C,B) ³ d (A,B) El
espacio Euclidiano de n dimensiones se simboliza con En |
||||||||||||||
| entorno circular |
Entorno
circular del punto A (a,b) y radio r es el disco abierto de radio r y centro
A(a,b) es decir es el conjunto de puntos del E2 { P(x,y) / (x-a)2 + (y-b)2 < r2 } o sea la d(P,A) < r Se simboliza con N (A,r) |
||||||||||||||
| entorno circular reducido |
Entorno circular reducido del punto A(a,b) y radio r es el disco abierto de radio r y centro A(a,b) excluyendo el punto A(a,b), es decir es el conjunto de puntos del E2 tal que : { P(x,y) / 0 < (x-a)2 + (y-b)2 < r2 } o sea la 0 < d(P,A) < r y se simboliza con N ' (A,r) |
||||||||||||||
| entorno rectangular |
Entorno rectangular del punto A(a,b) y semiamplitud "d" es el conjunto de puntos P(x,y) del E2 tales que verifiquen : | x - a | < d | y - b | < d |
||||||||||||||
| entorno rectángular reducido |
Es el mismo que el anterior pero excluyendo el punto A(a,b) es decir es el conjunto de puntos P(x,y) del E2 tales que 0 < | x - a | < d 0 < | y - b | < d |
||||||||||||||
| exterior de un conjunto |
Es el conjunto formado por todos los puntos exteriores de un conjunto dado |
||||||||||||||
|
existencia y unicidad, condiciones de |
Determinadas condiciones que garantizan la existencia de al menos un elemento y que además ese elemento es único o sea no hay otro igual |
|
|
|
|
|
|