Extracto del Libro: de Martín Garner - Circo Matemático - Alianza Editorial
Año 1979 - Pág. 134 a 147
Números Cíclicos:
El número 142.857, que los numerólogos y aficionados a la aritmética recreativa sin duda habrán reconocido en el acto, es uno de los enteros más curiosos. Pues, aparte del número 1, donde la prioridad es trivial, es el menor de los números cíclicos. Un número cíclico es un número entro de "n" cifras que presenta la insólita característica de que al multiplicarlo por cualquiera de los números comprendidos entre 1 y "n"( cantidad de cifras del número) , ambos inclusive, el producto tiene la misma cantidad de cifras que el número original, y los mismos valores, solo que alteradas las posiciones, pero respetando el orden cíclico de éstas.
Imaginemos un collar cuyas cuentas fuesen los números, repetidos hasta cerrar el círculo: 142857142857142857142857142857142857...
Podemos abrir el collar en seis sitios distintos, por ejemplo en la tercer posición, y a partir de la cuarta resulta : 857142857142857142857142.....
Así, obtenemos seis series distintas de las seis permutaciones cíclicas del número escrito, esto también se puede ver calculando los productos:
1 x 142857 = 142857
2 x 142857 = 285714
3 x 142857 = 428571
4 x 142857 = 571428
5 x 142857 = 714285
6 x 142857 = 857142
La naturaleza cíclica de estos 6 productos ha venido intrigando desde hace mucho a los ilusionistas. Muchos finos trucos de predicción matemática se inspiran en ellos. He aquí uno que describiremos: Preparamos una baraja francesa, de 52 naipes, empezando por separa las 9 picas cuyo valor se expresa con una sola cifra ( las de valores 1 a 9). Estas cartas son colocadas en la parte inferior del mazo, de manera que su orden, de abajo a arriba, sea 1 - 4 - 2 - 8 - 5- 7 ; a continuación van las tres cartas restantes en cualquier orden: 3 - 6 - 9 . Anunciamos que el resultado de nuestro acto mágico será el número 142857 , que aparecerá escrito con grandes cifras en una tira de papel metida en un sobre cerrado. Cortamos una tira de papel de longitud doble a la del sobre que la contendrá y escribimos en el ella el número antes mencionado y pegamos sus extremos de manera tal que se forme una faja circular.
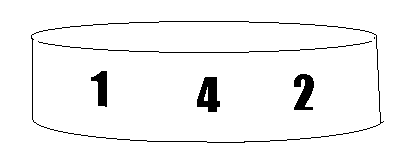
Después la aplanamos, y así plegada la metemos en el sobre, que cerramos y pegamos. Como es obvio, tenemos que saber de memoria el número 142857 y también recordar que sus tres primeras cifras están en la mitad superior de la Banda, y las otras tres, en la mitad inferior. Más tarde abriremos el sobre, cortándolo con unas tijeras por uno de los cuatro lugares marcados con A , B , C , D . Si se corta por A o por D, córtese también la extremidad de la banda de papel, con lo cual, al extraerla, quedará una tira rectangular que mostrará el número 142857 o bien el 857142 .
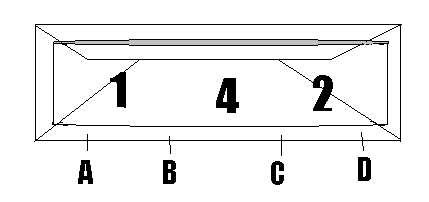
Para obtener las otras dos permutaciones basta proceder de igual manera por el reverso del sobre. Esta idea de cortar el sobre y extraer de el una tira de papel que exhiba una de las seis permutaciones cíclicas de 142857 está inspirada en un sistema inventado por Samuel Schwartz, un abogado neoyorquino, ilusionista aficionado. Schwartz, se vale de un sobre comercial, de los que muestran una ventana transparente, por la cual los espectadores pueden ir viendo las cifras; además su forma de preparar el mazo es ligeramente distinta, pero su método es, en esencia, idéntico al explicado.
Al empezar el truco se les entrega el sobre que contiene nuestra predicción. Le damos a otra persona el mazo ya preparado, le pedimos que lo baraje a fondo, "peinándolo" dos veces. Es decir el mazo se divide en dos partes sensiblemente iguales y las cartas se mezclan dejándolas escurrir por los pulgares. El doble peinado hará que las nueve cartas queden repartidas por el interior de la baraja, haciéndola subir por el interior del mazo, pero sin modificar el orden de las picas. Seguidamente, le explicamos al auditorio que vamos a construir un número de seis cifras sacadas al azar y que para ello volveremos el mazo boca arriba y tomaremos de el las seis primeras picas cuyo valor sea de una sola cifra. Naturalmente que el resultado será 142857. Colocamos esta carta en hilera sobre la mesa y lanzamos un dado para tener también un multiplicador al azar, de 1 a 6. Entonces se multiplica el número 142857 por el que halla salido. Luego se abre el sobre por el lugar correspondiente, haciendo un corte en A, B, C, etc como ya se explicó y se saca a la vista la tira de papel dejando de manifiesto la exactitud de la predicción.
Este número 142857, interviene en otros muchos trucos de ilusionismo, empero, tienen el defecto de que los espectadores pueden acabar dándose cuenta de que el número es el mismo. Por otra parte este número es ya muy conocido. Una forma de dificultar este conocimiento consiste en valerse de dicho número dividido por alguno de sus divisores como son 3,9 u 11.
Hace muchos siglos cuando los matemáticos cayeron en la cuenta del carácter cíclico de 142857, empezaron a buscar otros números mas grandes que tuvieran esta misma antojadiza propiedad. Los primeros trabajos encaminados a este fin pueden verse resumidos en el primer volumen de: History of Theory of Numbers, de Leonard Eugene Dickson , capítulo VI; desde los tiempos de la primera edición de Dickson, en 1919, se han escrito docenas de artículos dedicados al tema. Resulta que todos los números cíclicos son los períodos de la expresión decimal de las fracciones recíprocas de ciertos números primos. La fracción recíproca de 7 es 1/7, y genera el decimal ilimitado: 0,142857142857142857... observemos que el número de cifras del período, es igual a un valor menos que 7 denominador de la fracción generatriz, (7-1) = 6, con lo cual tenemos un procedimiento para descubrir otros números cíclicos mayores. En el caso que sea p un número primo, 1/p será la fracción generatriz si resultase de ella un número decimal periódico cuyo período estuviera compuesto por p-1 cifras, tal período sería un número cíclico.
El siguiente número primo que genera un número cíclico es 17, ya que 1/17 = 0,588235294117647588235294117647... que consta de 16 cifras.
Multiplicando este número: 588235294117647 por cualquier otro comprendido entre 1 y 16, se reproducen las 16 permutaciones cíclicas de este número. todos los números cíclicos engendrados por números primos mayores que 7, empezarán por 1 o varios ceros. y en el caso de que los utilicemos para trucos de predicción o exhibiciones de cálculos rápidos, podremos prescindir de los ceros iniciales, necesariamente acordándonos luego de insertarlos en los lugares oportunos del producto definitivo.
Entre los números primos menores que 100 hay exactamente 9 que generan números cíclicos que son: 7, 17, 19, 23, 29, 47, 59, 61, 97. Durante el siglo pasado se descubrieron otros muchos números cíclicos de longitudes muy superiores a las 96 cifras y en la actualidad con la ayuda de la informática, se conocen hasta los que tienen 600 cifras. Williams Shanks, famoso por haber calculado las primeras 707 cifras decimales del número PI (quien cometiera un error en su calculo en la cifra del lugar 528 y sucesivas) descubrió un número cíclico generado por 1/17389 y determinó correctamente las 17.388 cifras del mismo.
Ninguna fracción con denominador "d" puede tener periodo formado por más de "d-1" cifras. Para lograr estos períodos de longitud máxima es condición necesaria que el número "d" sea primo. Resulta así que los números cíclicos equivalen a periodos de longitud máxima de fracciones recíprocas de números enteros. Es fácil comprender porque la máxima longitud del periodo es d-1". Pues al ir dividiendo 1000 entre "d", en cada etapa del proceso de división hay solamente "d-1" restos posibles distintos de 0; tan pronto se repita un resto comenzaran a repetirse las cifras del cociente y aparece el periodo.
También es fácil ver el motivo de que estos periodos de longitud máxima sean cíclicos. Fijémonos por ejemplo en 8/17. Puesto que al dividir 1/17 se presentan ya todos los restos posibles, al dividir 8 entre 17 no hacemos mas que comenzar el proceso cíclico en lugar diferente. Es seguro entonces que obtendremos en el periodo del nuevo número decimal las mismas cifras que antes, y en el mismo orden cíclico. Al multiplicar por 8 el número cíclico generado por 1/17 no hacemos mas que hallar el periodo de 8/17; por lo tanto el producto tendrá que ser permutación cíclica de los mismos 16 dígitos que forman el periodo de 1/17.
No se dispone de ninguna formula explicita, no recursiva, capaz de generar automáticamente todos los números primos cuyas fracciones reciprocas sean generatrices de números cíclicos. Puesto que tampoco son todos los números primos, sin embargo hay muchas "mañas" que simplifican grandemente la tarea de identificar tales primos y de generar métodos para poder programar ordenadores que puedan determinarlos. No se sabe aun si existen infinitos primos capaces de generar números cíclicos, pero tal conjetura parece bastante verosímil. En la valiosa tabla de periodos de los recíprocos de los números primos preparada por Samuel Yates y que incluye todos los números primos menores o iguales que 1.370.471 alrededor de las 3/8 partes de los números primos allí estudiados son cíclicos. La proporción permanece sensiblemente constante al ir tomando muestras de distintos segmentos de la tabla, por lo que la conjetura de validez para todos los números primos no parece descabellada.
Al multiplicar un número cíclico por el número primo que lo engendra, el producto es siempre un hilera de nueves. Por ejemplo 7 x 142857 = 999999. Disponemos entonces de otro método para buscar números cíclicos consistente en: tomar el número "p" primo, y se va dividiendo una hilera de nueves entre "p" hasta lograr un resto 0. En el caso de que el cociente tenga "p-1" cifras, hemos encontrado un cíclico.
Todavía mas inesperada es la propiedad de que al escindir por la mitad el bloque de cifras que compone el número cíclico (o cualquiera de sus permutaciones circulares) los dos números resultantes dan al sumarlos, una hilera de nueves. Por ejemplo: 142 + 857 = 999 o bien el número cíclico 0588235294117647 engendrado por la fracción 1/17, si lo escindimos por la mitad resulta: 05882352 + 94117647 = 99999999. Tan sorprendente propiedad es caso particular del "Teorema de Midy", atribuido por Dickson a E. Midy, quien lo dio a conocer en Francia en 1836. Este teorema enuncia que si el periodo de la expresión decimal de a/p (siendo p un numero primo) consta de un numero par de dígitos, entonces, la suma de los dos números obtenidos al escindir el periodo en dos bloques iguales será una hilera de nueves. Sin embargo hay números primos como el 11, por ejemplo, cuyos periodos tiene longitud par, no son cíclico, y cumplen esta propiedad de los nueves. Algo que hay que destacar es que en todos los números cíclicos conocidos hasta hoy son de longitud par de cifras, por lo tanto el teorema de Midy se cumplirá para todos ellos.
Esta propiedad conviene recordarla pues permite determinar un método para obtener números cíclicos consistente en tomar el numero primo y ver si genera un numero cíclico por el método de la división (descrito anteriormente) pero que será suficiente hacerla hasta la mitad del número, las cifras que faltan pueden obtenerse rápidamente sin mas que tomar los complementos a nueve de las ya obtenidas.
Evidentemente, resulta también del teorema de Midy que todos los números cíclicos habrán de ser múltiplos de nueve pues esta claro que lo es la, suma de sus cifras.
Los lectores a quienes interesa una demostración elemental del teorema de Midy pueden consultar The Ejoyment of mathematics, por Hans Rademacher y Otto Toeplitz (Pricenton University Press, 1957), pp. 158-60. [Hay traducción española, Números y figuras, Alianza editorial, Madrid, 1970]. Y puede verse otra demostración, debida a W. G. Leavitt, "A theorem or repeating decimals", en The American Mathematical Monthly, junio-julio de 1967, pp. 669-73.
Los números cíclicos tienen otras muchas extrañas propiedades; quizás el lector pueda tener el placer de descubrir algunas por si mismo.
Aquí tan solo mencionare otra mas: todo numero cíclico puede se engendrado de multitud de formas: como suma de un progresión geométrica infinita, escrita en diagonal.
Por ejemplo, tomemos 14 como valor inicial y vayamos duplicándolo en cada paso escribiendo los números resultantes de forma que sobresalgan cada vez dos cifras a la derecha:
| 1 | 4 | ||||||||||||
| 2 | 8 | ||||||||||||
| 5 | 6 | ||||||||||||
| 1 | 1 | 2 | |||||||||||
| 2 | 2 | 4 | |||||||||||
| 4 | 4 | 8 | |||||||||||
| 8 | 9 | 6 | |||||||||||
| .... | ... | ||||||||||||
| 1 | 4 | 2 | 8 | 5 | 7 | 1 | 4 | 2 | 8 | 5 | 7 | 1 | 4.. |
En la suma va repitiéndose el número cíclico mínimo (no trivial).
Otro procedimiento para obtener el mismo número cíclico es empezar por 7 e ir moviéndose uniformemente hacia la izquierda, multiplicando en cada paso por 5 el número anterior, y conservando, las cantidades obtenidas ceñidas a la diagonal por su lado derecho:
| 7 | |||||||
| 3 | 5 | ||||||
| 1 | 7 | 5 | |||||
| 8 | 7 | 5 | |||||
| 4 | 3 | 7 | 5 | ||||
| .. | .. | .. | .. | ||||
| .. | .. | 1 | 4 | 2 | 8 | 5 | 7 |
Se sabe que existen números cíclicos de orden 1, que son de los que estuvimos hablando y los de orden 2 que no son verdaderamente cíclicos como el generado por la fracción 1/13, resultando 076923. Estos abren nuevos campos de investigación como por ejemplo los cuadrados mágicos que generan o las relaciones con la series famosas como: el cíclico de orden 2 engendrado por 89 y la serie de Fibonacci.
El teme de los números cíclicos de orden mayor que 1 es una espesa jungla, y la literatura dedicada a él se encuentra dispersa acá y allá, faltando por hacerse una bibliografía sistemática. Idénticas observaciones valen para los números cíclicos de base distinta de 10, como por ejemplo base 2, base 8, etc. que no detallaremos en este texto.