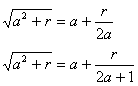| A |
Primera letra del abecedario de mayúsculas, utilizada para indicar nombres de conjuntos o nombres de matrices. Los romanos primitivos le asignaban el valor 500 que posteriormente asumió la D.- |
||||||||||
| a |
Primera letra del alfabeto en minúsculas, se utiliza para designar elementos de un conjunto o una cantidad constante cualquiera, en el sistema métrico representa a la unidad de área (a).- |
||||||||||
| µ |
Primera letra del alfabeto GRIEGO en minúsculas, se utiliza para designar ángulos o coeficientes. En el primitivo sistema de numeración griega representaba la unidad.- |
||||||||||
| À |
Primera letra del alfabeto hebreo( Alef), que GEORG CANTOR propuso, y se acepta universalmente, para designar los números cardinales transfinitos. Es también la inicial en hebreo de la palabra alemana: abzählbar que significa numerable.- |
||||||||||
| Aamulí |
Behaeddín Mohámed Abenhusain, matemático sirio que vivió en el período (1547-1622), que escribió una obra de Aritmética y Álgebra traducida al alemán por Nesselman:"Essenz der Rechenkunst von Mohamed Beha-eddin ben Alhosain aus Amul, Berlín, 1843, en la que se ocupa de la regla de doble falsa posición, que llama "Regla de los platillos de la balanza", y de la suma de progresiones, entre ellas la de los números pares y la que con nuestra notación es:
|
||||||||||
| abacista |
Calculador con el ábaco. Sinónimo, en la Edad Media de aritmético, especialmente entre los siglos XI y XVI, durante los cuales la aritmética estaba casi reducida a las operaciones que se podían realizar con dicho instrumento. |
||||||||||
| ábaco |
Del griego abae, tabla, del latín abacus, cuadro. Aparato usado antiguamente para facilitar los cálculos, y que puede considerarse tan viejo como la aritmética. Su forma varió con el tiempo, adaptándose su disposición a las necesidades del sistema de numeración usado en cada pueblo. El ábaco primitivo era un tablero rectangular sobre el cual se extendía una capa de polvo- y de allí la posible etimología del hebreo abak, polvo - en la que el calculador escribía con el dedo o con un estilete, los signos que representaban los números, haciendo luego las cuentas por medio de piedrecillas. Sinónimo de nomograma |
||||||||||
| ábaco cartesiano |
Nombre dado por Pouchet al nomograma representado en un sistema de coordenadas cartesianas x, y que resulta de transformar la función de tres variables f ( z1 , z 2 , z3)=0 por medio de la sustitución de x = m1z1 ; y = m2z2, que en el sistema equivalente toma la forma:
f ( z1 , z 2 , z3)=0 . La construcción de éstas no es fácil, en muchos casos, pero se consigue mediante la anamorfis. Ver anamorfis.- |
||||||||||
| ábaco chino |
Análogo al romano, tanto por su construcción como por su manera de usarlo. Se diferencia de él, que en vez de tener las bolas en surcos, están ensartadas en tallos de bambú, y se divide en dos partes desiguales por medio de un travesaño que deja dos bolas en la parte menor y cinco bolas en la parte mayor. Cada una de las bolas, representan cinco unidades, y las cinco bolas de la parte mayor una unidad cada una de ellas, de modo que acercando al travesaño una bola de las de valor cinco y cuatro de las de valor uno, se tiene la suma de 5 + 4 . |
||||||||||
| ábaco de puntos alineados | |||||||||||
| ábaco exagonal |
Teniendo en cuenta que el logaritmo de un producto es la suma de los logaritmos de los factores, y tomando el mismo módulo sobre los ejes, la ecuación: f1+f2=f3
[1] , se puede representar por tres haces de rectas paralelas: las
verticales x=mf1 ; las horizontales y=m f2 y
las oblicuas x + y=m f3 , de 45° de inclinación,
perpendiculares a la bisectriz del ángulo de los ejes sobre la cual
determinan la escala funcional mf3 /
El nomograma se utiliza orientando el transparente de manera que sus tres índices sean normales a las tres escalas y corriéndolo hasta que sus tres índices perpendiculares a las escalas de los datos pasen por los puntos de estas escalas cuyas cotas tengan por valores estos datos, y entonces el tercer índice cortara a la tercer escala en un punto cuya cota es la solución. Para que las tres escalas tengan el mismo modulo basta tomar como eje los lados de un ángulo de 120°, conservando perpendiculares a ellos las z1 y z2 , porque de este modo las z3 determinan en la bisectriz del ángulo de los ejes la escala t = m f3. La ecuación [1], se puede representar sin necesidad de dibujar las líneas z1 , z2 y z3, siempre que se aplique, sobre el plano de las tres escalas, un transparente móvil, de orientación fija, con tres índices concurrentes que coincidan con las z1 , z2 y z3 en toda posición del mismo, en cuyo caso las tres escalas quedan paralelas a los lados de un triangulo equilátero y los índices del transparente son las tres diagonales de un hexágono regular, por lo que Lallemand llamó hexagonales a éstos ábacos. |
||||||||||
| ábaco japonés |
Es simplemente una modificación del chino, consta de veinte filas divididas también por un travesaño en dos partes desiguales, en la mayor de las cuales hay cinco bolas ensartadas, pero en la menor solo una en vez de dos. |
||||||||||
| ábaco peruano | |||||||||||
| ábaco romano |
Rectángulo de madera, mármol u otra sustancia, dividido por surcos paralelos sobre los cuales se pueden deslizar fichas que primero fueron guijarros pulimentados, después huesos y finalmente discos metálicos: de palat y de oro los más lujosos. Al primitivo abaco romano se le agregaron dos varillas marginales con cuatro y doce fichas respectivamente para facilitar las sumas de cuartos y dozavos de la unidad |
||||||||||
| ábaco ruso |
Variedad del ábaco romano, de varillas marginales, las cuales tienen en el ruso, diez fichas o bolas. Ver: nomograma |
||||||||||
| abatimiento | |||||||||||
| abatir | |||||||||||
| Abdank-Abakanovicz, Bruno |
Polaco(1852-1900) que inventó en 1878, el integrador mecánico. |
||||||||||
| abducción |
Silogismo cuya premisa mayor es cierta y la menor probable, de modo que la conclusión solo puede ser probable.- |
||||||||||
| Abel, Lema de |
Sean una sucesión (an) de elementos de un espacio vectorial normado y completo E y un número complejo z0 tales que la sucesión (z0n an) esté acotada. Bajo estas condiciones el lema de Abel nos asegura que la serie entera ån = 0¥ z0nan en todo es absolutamente convergente en la bola abierta de centro 0 y de radio |z0| y normalmente convergente conjunto compacto que esté contenido en esta bola. |
||||||||||
| Abel, Niels Henrik |
|
||||||||||
| Abel, regla de |
Consideremos una sucesión (an) de números reales positivos y una sucesión (an) de elementos de un espacio vectorial normado y completo E. Si se cumplen las siguientes condiciones:
Entonces la serie ån = 0¥ an an converge y además para todo entero no negativo n se cumple la siguiente fórmula de acotación del resto:
|
||||||||||
| Abel, teorema de |
n
= 0¥znan
con radio de convergencia R > 0.
Sea también z0 un número complejo tal que la
serie å
n = 0¥z0n
an converge. Entonces para todo número real a
Î [0,p/
2], la aplicación
tiende a f(z0) cuando z tiende a z0 siempre que z quede dentro de la intersección de la bola cerrada de centro 0 y radio R y del sector angular definido por arg(-z0)-a £ arg (z-z0) £ arg(-z0)+a . |
||||||||||
| abeliana, integral |
Sea R(x,y) una función racional de dos variables y supongamos que y = f(x) (es decir, que la variable y es función de la variable x) y que existe una relación polinómica del tipo P(x,y) = 0 entre x e y. Entonces una primitiva de la restricción fy(x) = R(x,y) se dice que es una integral abeliana. Las integrales elípticas y las hiperbólicas son casos particulares de integrales abelianas. |
||||||||||
| abeliano, grupo | |||||||||||
| Abenalbana |
Abulabbás Abenmohámed, llamado Abenalbana - el
hijo del arquitecto- nació y murió en Marruecos ( 1256-1323); se educó en
Fez y escribió numerosas obras, las más famosas de las cuales son un tratado
de Álgebra en donde estudia las expresiones de la forma
según que sea r £ a ó r > a : la descomposición en factores primos, y el siguiente criterio de divisibilidad por 7, bastante más sencillo y práctico que el que se expone en los manuales : Si se multiplica la primera cifra de la izquierda de un número por 3 y se le suma la segunda cifra, el resultado se multiplica por 3 y se le suma la tercera cifra y así sucesivamente, el resultado final y el número propuesto dan el mismo resto al dividirlos por 7.- |
||||||||||
| Abenbéder |
Probablemente sevillano, Abuabdala Mohámed Benomar, vulgarmente conocido por Abenbéder, floreció entre los siglos XII y XIII, y es autor de un notable tratado de Álgebra cuyo manuscrito, que se conserva en el Museo del Escorial ( España), ha sido traducido por Sánchez Pérez, Madrid, 1916. En la edición de éste, así como en sus obras Biografía de matemáticos árabes que florecieron en España, Madrid, 1921 y Las Matemáticas en la Biblioteca del Escorial, Madrid, 1929, y en la Francisco Vera: Las matemáticas de los Musulmanes Españoles, Buenos Aires, 1947, pueden verse detalles acerca de la vida y la obra de Abenbéder.- |
||||||||||
| Abendaud, Salomón |
Nombre de un sefardí, probablemente de Sevilla, que lo cambió por el Juan Hispalance al convertirse al cristianismo. Floreció en el siglo XII y tradujo en la ciudad de Toledo ( España) varias obras matemáticas que tuvieron gran difusión. |
||||||||||
| Abenesra, Abraham |
Polígrafo sefardí, de Toledo ( España).nacido en el año 1092; viajó por África, Palestina, Italia, Francia e Inglaterra y escribió un Sepher ha-Mispar o Yesod Mispar, tratado de aritmética con reminiscencias pitagóricas, pero también con algunos teoremas sobre suma de cuadrados y raíces cuadradas, y un Liber augmenti et diminutions , publicado por Libri, en el que habla de un Método de sustitución - regula infusa - estudiado posteriormente por David E. Smith en su History of Mathematics, Boston, 1925. Murió en Roma el año 1167.- |
||||||||||
| Abenyunus |
Astrónomo egipcio ( 979 - 1008) que tradujo a Diofanto y escribió un Almagesto, por lo que algunos lo confunden con Ptolomeo. Corrigió algunas fórmulas de este, y la Trigonometría le debe la que con notación moderna es: cos a . cos b = 1/2 [cos (a+b) + cos (a-b)] |
||||||||||
| Abraham Bar Hiia |
Cuyo apodo era Savasorda, judío español que nació por los años 1070, y con el cual se le conoce. Es una corrupción de Sáhib el Xorta- jefe de la guardia- porque tal vez sirvió en alguna corte musulmana. Escribió un Sépher hibbur hameixihá uehatixbóret: Libro del tratado de la medida y del cálculo, traducido con el título de Liber Embadorum por Platón de Tívoli y modernamente al catalán por Millás Vallicrosa: Llibre de Geometria de Abraham bar Hiia, Barcelona, 1931, y en él se encuntra por primera vez la ecuación de segundo grado, siendo por tanto, el verdadero introductorde ésta en Europa, y no Leonardo de Pisa, que ha venido detentando este honor.- |
||||||||||
| abierta,
aplicación |
Una aplicación f: E® F entre dos espacios topológicos E y F se dice abierta, si la imagen por f de todo subconjunto abierto de E es un subconjunto abierto de F. |
||||||||||
| abierto | |||||||||||
| abscisa |
Del latín abscindere, cortar. Número que mide una distancia.-Ver cartesiano, sistema de referencia, coordenadas.- |
||||||||||
| abscisa curvilínea |
Distancia desde un punto de una curva orientada, tomado como origen, a otro punto de la curva, medida a lo largo de ésta. Si la curva es cerrada, un mismo punto puede tener, evidentemente, infinitas abscisas; y así por ejemplo, la abscisa curvilínea del punto B, siendo A su origen, es la longitud del arco AB, medida en grados, en radianes, en metros, etc... y también
|
||||||||||
| absoluto, valor |
Del latín absolutum, lo que no tiene nexo, relación, limitación o dependencia, y así se habla en Matemática del Valor Absoluto de un número, de un error o de la Función Valor Absoluto.- Sea A un anillo. Un valor absoluto es una aplicación de A en el conjunto de los números reales no negativos
que cumple las condiciones siguientes:
|
||||||||||
| absoluto del espacio | |||||||||||
| absoluto del plano | |||||||||||
| abstracción | |||||||||||
| abstracto |
Cualidad que excluye el sujeto. En ciertos órdenes de ideas, este concepto es sinónimo de General; pero en Matemática no es admisible esta identificación de conceptos. Por ejemplo: los conceptos de número y fracción, son ambos abstractos, pero el primero es más general que el segundo, puesto que lo comprende como caso particular. |
||||||||||
| abstraer |
Del latín abs-trahere: atraer, tirar hacia sí. Considerar por separado las cosas que están relacionadas de tal modo que no se pueden dar en forma aislada. Es, por tanto, la operación intelectual que descompone una idea en elementos inseparables, so pena de destruirla. La longitud de una circunferencia, por ejemplo, es un número y no una línea recta o curva, como también es un número el área de un circulo, el cual se puede concebir, por abstracción, sin la circunferencia que es su contorno. |
||||||||||
| absurdo | Contrario a la razón. En sentido estricto es la incompatibilidad de dos proposiciones contradictorias, que no pueden ser simultáneamente verdaderas, ni simultáneamente falsas. | ||||||||||
| absurdo,
demostración por reducción al |
Es un tipo de prueba matemática que consiste en suponer, la negación de la proposición a demostrar y deducir de tal suposición la veracidad de un enunciado Q y su negación no Q. |
||||||||||
| Abucámil |
El algebrista egipcio Abensoga Abenaslam, conocido por Abucámil, floreció a principios del siglo X. Tuvo gran fama de calculador; aplicó el Algebra Geométrica de los griegos a la resolución de ecuaciones; conocía la identidad de
muy útil cuando a y b son cuadrados perfectos; hizo muchas aplicaciones de la regla de falsa posición ( Regula Falsi) y ejerció influencias en Europa, según se desprende del trabajo que le dedicó Suter: Das Buch der Seltenheiten der Bechenkunst von Abu Kamil El-Misri, publicado en la Bibliotheca Mathematica de Enestrom, tomo XI, 1910 - 1911. Karpinski ha traducido su Algebra: The Algebra of Abu Kamil Shoja, en la misma revista, tomo XII, 1911- 1922. |
||||||||||
| Abulguafa |
Floreció en Oriente entre los años 933 y 998. A él se debe el concepto correcto de tangente trigonométrica que llamó sombra invertida, definiendo su inversa , la cotangente, como sombra recta. Perfeccionando los resultados obtenidos por Albatenio, y partiendo de la desigualdad
Calculó el valor de sen 30 ° en menos de 1/ 10 9 del radio, y construyó una tabla de valores naturales de senos de 10 en 10 minutos. Abulguafa fué uno de los últimos grandes traductores de los matemáticos y astrónomos griegos, y comentó a Euclides, Diofanto y Ptolomeo.
|
||||||||||
| academia |
Sociedad de científicos, artistas o literatos. El nombre se deriva del Academos, héroe griego en nombre de quien consagraron en Atenas unos jardines, en los cuales se instaló Platón para exponer su Filosofía. |
||||||||||
| academia florentina |
La fundada por Cosme de Médicis, en Florencia (Italia) en el año 1442 a instancias del filosofo bizantino Gemistos Plethon para el estudio de Platón. Desde el punto de vista matemático fue tan estéril como lo de Atenas. |
||||||||||
| academia platónica |
Fundada en Atenas por Platón en el año 387 antes de J.C., defendió el carácter exclusivamente intelectual de la Matemática "apoyándose en ideas puras por las que empieza, procede y concluye la demostración", es decir: un análisis regresivo que determina , a través de las gradaciones sistemáticas de una teoría del conocimiento, la creciente intensidad de la actividad mental, que le hace crear a un tiempo mismo una Filosofía matemática y una Matemática filosófica. El enfermizo idealismo de Platón y el aislamiento del mundo que le permitía s posición social, hizo que la academia se contaminara con las extravagancias místicas y religiosas que culminaron en el Timeo, donde se advierte un total desconocimiento matemático. |
||||||||||
| acción, ley de |
Sean G y E dos conjuntos no vacíos. Una ley de acción de G sobre E o ley de composición externa sobre E es una aplicación de G×E en E. |
||||||||||
| aceleración |
Se define como: la variación de la velocidad por unidad de tiempo. Tiene gran interés en Física el estudio de la función cuya variable es el tiempo; y así la función "espacio recorrido" es:
el movimiento es uniformemente acelerado o retardado si es
Si la variación no es constante, la aceleración es la derivada segunda del espacio respecto del tiempo. Tomando por unidad de tiempo, el segundo y por unidad de longitud el metro, la aceleración es g y, por consiguiente, es v' = g. Como las únicas funciones que tiene esta derivada son v = gt + ß, siendo ß una constante cualquiera, es y' = gt + ß, que es la derivada de
siendo g una constante cualquiera; luego esta función, y lo mismo la g = at2 + bt + g , son la expresión general de todos los movimientos uniformemente acelerados, siendo ß la velocidad inicial en el momento t = 0 y g la abscisa inicial para el instante t=0. Por ejemplo: lanzando una piedra con una velocidad inicial de 30 metros por segundo desde 5 metros de altura, es b= ±30, según que la piedra se lance hacia arriba oy hacia abajo y g = -5, tomando como sentido positivo el de la gravedad, luego la ecuación del movimiento será:
Si tomamos el valor aproximado de g =10 metros por segundos al cuadrado, el momento de caída al suelo esta dado por la ecuación:
En el movimiento curvilineo, si el punto P describe una curva alabeada engendrada por el vector móvil OP, la aceleración es la derivada del vector velocidad; vale, por lo tanto,
La aceleración está situada en el plano osculados de la trayectoria del punto P. |
||||||||||
| aceleración normal |
En el movimiento curvilineo, es la componente de la aceleración, dirigida según la normal, en el sentido de la concavidad de la trayectoria que describe el punto que engendra la curva. |
||||||||||
| aceleración tangencial |
Variación de la velocidad absoluta o incremento de la velocidad en la unidad de tiempo, dirigido según la tangente. |
||||||||||
| Ackermann, Wilhelm |
Alemán contemporaneo, que sigue la trayectoria de Hilbert, expuesta en Hilbert- Ackermann: Grunzuge der theoretischen Logik, Berlín, 1928.- |
||||||||||
| acorde | |||||||||||
| acotación de errores | |||||||||||
| acotación de la integral | |||||||||||
| acotación de la raíces de una ecuación | |||||||||||
| acotada, medida |
Supongamos que E es un espacio topológico localmente compacto y que m es una medida sobre E. Si tal medida es positiva y además la función constante e igual a 1 es m-integrable, entonces se dice que la medida está acotada. Si la medida m es real, diremos que está acotada si sus partes positiva y negativa lo están. En el caso de que la medida m sea compleja se dirá que es acotada si sus partes real e imaginaria lo son. |
||||||||||
| acotado |
Un subconjunto A de un conjunto ordenado M se dice acotado si está mayorado y minorado. Una parte de un espacio vectorial normado se dice acotada si está contenida en alguna bola cerrada del espacio. Una aplicación f de un conjunto E en un conjunto ordenado M está acotada si su imagen f(E) es una parte acotada de M. |
||||||||||
| acre |
Medida agraria inglesa equivalente a 4046,8 metros cuadrados |
||||||||||
| acumulación de errores | |||||||||||
| acumulación,
punto de |
Sea A un subconjunto de un espacio topológico E. Decimos que un punto xÎ E es de acumulación de A si todo entorno de x contiene puntos de A distintos del propio x. |
||||||||||
| acutángulo | |||||||||||
| Adams, John Crouch |
Astrónomo inglés (1819-1829), que calculó la constante de Euler con doscientas setenta y tres cifras exactas. |
||||||||||
| adarme |
Del árabe ad-derhem , nombre genérico de toda moneda pequeña de plata y específico de una de ellas. Como medida de peso, equivale a 1,79 gr. |
||||||||||
| adherente, punto |
Sea A una parte de un espacio topológico E. Un punto x Î E es adherente a A si todo entorno de x tiene puntos de A. Obviamente, todo punto de acumulación es adherente pero lo recíproco no es cierto. |
||||||||||
| adición |
Ley de composición interna en un conjunto E denotada por el símbolo +. Se suelen notar aditivamente sólo aquellas leyes que resulten asociativas y conmutativas. Operación de suma |
||||||||||
| adición de ángulos |
Si dos o más ángulos planos o diedros, ordenados en el mismo sentido, son tales que el lado inicial del segundo ángulo coincide con el lado terminal del primero, el ángulo determinado por el lado inicial del primero y el terminal; del segundo será el ángulo suma de los dos. De la congruencia de ángulos, se puede establecer que la suma de ángulos es conmutativa. Teniendo en cuenta que la condición necesaria y suficiente para que dos diedros sean iguales es que los sean sus secciones rectas, resulta que la adición de ángulos diedros se reduce a la adición de sus secciones rectas. |
||||||||||
| adición de cuaternios |
Teniendo en cuenta que cuaternios son números complejos de cuarto orden ( Véase cuaternios). La suma de dos cuaternios se establece con arreglo a la definición de esta clase de números complejos, aplicando la regla del paralelogramo a sus partes vectoriales y atribuyendo al vector resultante un peso equivalente a la suma de los pesos de los sumandos. |
||||||||||
| adición de desigualdades |
Véase Desigualdad y Leyes de Monotonía |
||||||||||
| adición de fracciones decimales |
Para la práctica de ésta operación, basta traducir las fracciones decimales a ordinarias, reducir éstas a un común denominador, aplicar las reglas para ello y escribir luego el resultado en forma decimal. Pero observando que dos decimales que tienen el mismo número de cifrasa la derecha de la coma representan dos frcciones ordinarias de igual denominador y si tienen distinto número de cifras decimales my n, ( m>n), se puede hacer que tengan el mismo número de cifras ,escribiendo m-n ceros a la derecha del que tiene menos. |
||||||||||
| adición de fracciones ordinarias |
Llamando suma de varias fracciones de igual denominador a la fracción que tiene por denominador el mismo que las fracciones dadas y por numerador a la suma de los numeradores de las fracciones dadas, y si las fracciones tienen distintos denominadores deberá obtenerse el COMÚN DENOMINADOR que se corresponde con el Mínimo Común Múltiplo de los denominadores a sumar, así:
|
||||||||||
| adición de igualdades | |||||||||||
| adición de infinitésimos |
La suma de un número finito de infinitésimos, es otro infinitésimo, porque siendo:
si tomamos todos los sumandos menores que
el valor absoluto del segundo miembro es menor que
La restricción de que sea finito el número de sumandos es fundamental, porque sin ella se podría afirmar por ejemplo, que es :
puesto que el límite de cada sumando es cero, y sin embargo basta observar para convencerse del error que, la suma de n sumandos vale 1, y como el límite de una constante vale la misma constante, esta suma tiene por límite a 1. |
||||||||||
| adición de monomios |
Se efectúa sumando los que sean semejantes entre sí y dejando indicada la suma entre los de distintos grados o partes literales, por ejemplo: 7a2b + 5a2b - 3a2b = 9a2b 2,5mn + 3,1m2n - 7,2mn2 + 1,3 mn - 0,5mn2 = = 3,8 mn + 3,1 m2n - 7,7 mn2 El resultado final de esta suma será en general un Polinomio, es igual a la suma de los valores numéricos de los monomios sumandos para todo sistema de valores atribuidos a sus letras |
||||||||||
| adición de números aproximados |
El caso más desfavorable en la adición de números aproximados es aquel en que todos ellos lo estén en el mismo sentido; de modo que si, por ejemplo, todos los sumandos están aproximados por defecto, y es S = A + B + C + ... + L la suma exacta, y S' = (A - a ) + (B - b) + (C - c) + ... + (L -l)
la aproximada, siendo a, b, c ... l los errores absolutos de los sumandos,
el error absoluto
si es a el mayor de todos los errores, es decir: El error absoluto de una suma de números aproximados es menor que el mayor de los errores de los sumandos multiplicado por el número de éstos. I. Para obtener la suma de varios sumandos, cuyo número no exceda de diez, en menos de una unidad de un cierto orden, basta tomar los sumandos por defecto con una cifra más, prescindir en la suma de la última cifra y aumentar la anterior en una unidad, pues en virtud del teorema anterior, el error absoluto de la suma es menor que diez unidades de su último orden, es decir: que una del penúltimo, y luego hay que incrementar en l la última cifra conservada. Si queremos, por ejemplo, calcular en menos de 0,01 la suma
tomando con tres cifras decimales los sumandos, resulta S' = 1,732 + 0,571 + 5,746 = 8,049 y, en virtud de la regla dada, es S' = 8,05. Si el número de sumandos es mayor que diez y menor que ciento, y, en general, está comprendido entre 10p y 10p+1, basta tomarlos por defecto con p cifras más de las que se quieran tener en el resultado. II. Dados varios sumandos, cada uno de los cuales esté aproximado en menos de una unidad del orden de su última cifra, para obtener el resultado con la máxima aproximación basta aplicar la desigualdad anterior
Así, si son exactas todas las cifras de los sumandos de la suma: S = 4,831 + 9,30845 + 27 + 8,74 , todos los errores son menores que 0,01; luego tienen exactas todas sus cifras los sumandos de la suma 4,83 + 9,30 + 27 + 8,74 = 49,87 , siendo menor que 4 x 0,01 = 0,04 el error de la suma. Por tanto, si suprimimos la cifra 7, el error es, entonces, menor que 0,04 + 0,07 = 0,11 < 1, y podremos asegurar que el número 49 tiene exactas todas sus cifras. |
||||||||||
| adición de números complejos |
Véase adición de vectores |
||||||||||
| adición de números fraccionarios | |||||||||||
| adición de números naturales |
Postularemos las leyes uniformes y conmutativa de la adición que dicen, respectivamente: Sumando miembro a miembro varias igualdades resulta otra igualdad y El orden de sumandos no altera la suma. En virtud de la ley conmutativa , se pueden colocar en primer lugar los sumandos que queramos, lo que equivale a sustituirlos por su suma efectuada, resultado que se enuncia en forma de ley así: En una suma se pueden sustituir varios sumandos por su suma efectuada. A esta ley, llamada asociativa, hay que agregar la de monotonía: Sumando miembro a miembro varias desigualdades del mismo sentido, se obtiene una desigualdad del mismo sentido. En efecto: si es a > b y c > d, es a = b + m y c = d + n; luego se tiene: a + c = b + d + m + n > b + d , y aplicando reiteradamente esta propiedad queda demostrada la ley. Si convenimos en que la ley conmutativa a + b = b + a sea válida para b = 0, resulta esta igualdad: a + 0 = 0 + a, y como por definición es a + 0 = a, se tiene: 0 + a = a , es decir: El cero como sumando no altera la suma. En la práctica de la adición se consideran tres casos: I. La suma de dos números de un cifra puede hacerse por agregación sucesiva de unidades, lo que se consigue con la llamada tabla de sumar: 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 13 5 6 7 8 9 10 11 12 13 14 6 7 8 9 10 11 12 13 14 15 7 8 9 10 11 12 13 14 15 16 8 9 10 11 12 13 14 15 16 17 9 10 11 12 13 14 15 16 17 18 De este modo la tabla resulta simétrica respecto de la diagonal 0-18 y la suma de dos números se encuentra en la intersección de las líneas iniciados por dichos números. II. En virtud de la ley asociativa, sumando un número de una cifra con el de las de otro de varias, resulta: a) Si la suma solo tiene una cifra, se coloca éstas en el lugar de las unidades y se conservan los demás guarismos del número de varios. Así, es 4875 + 5 = 4878, por ser 3+5 = 8. b) Si dicha suma tiene dos cifras, se coloca la de sus unidades en el primer lugar de la derecha, se aumenta una unidad la cifra de las decenas del número de varias, puesto que la suma parcial a lo más vale 9 + 9 = 18, y se conservan las demás cifras del número de varias. Por ejemplo: 5928+7=5935, habiendo asociado la decena que hay en 15 unidades a las 2 del sumando 5928 porque es 8 + 7 = 15. III. Finalmente, para sumar varios números de varias cifras, basta sumar, en virtud de la misma ley, las unidades, las decenas, las centenas, etc., de los sumandos, y si alguna de estas sumas parciales tiene más de una cifra, se escribe solamente la primera de la derecha, asociando las demás a las de su mismo orden. Así, por ejemplo, tenemos: 458 + 5821 + 47 + 2 = (8 + 1 + 7 + 2)unidades + (5 + 2 + 4) decenas + (4 + 8) centenas + 5 millares = 18 unidades + 11 decenas + 12 centenas + 5 millares = 8 unidades + 12 decenas + 12 centenas + 5 millares = 8 unidades + 2 decenas + 3 centenas + (1 + 5) millares= 8 unidades + 2 decenas + 3 centenas + 6 millares = 6328. En la práctica conviene colocar los sumandos unos debajo de otros, de modo que formen columna las unidades del mismo orden. |
||||||||||
| adición de números negativos |
Representando los números negativos por pares ordenados de números naturales (a1, a2) , (b1, b2) ... , se llama suma de dos números negativos al que se obtiene así: (a1, a2) + (b1, b2) = (a1+ b1 , a2+ b2). En la representación gráfica de los números negativos por puntos alineados en una semirrecta, se observa que sumar equivale a contar hacia la derecha [izquierda] del origen con la unidad positiva [negativa]. Si contamos con -1 a partir de 0 hacia la izquierda, alcanzaremos el mismo número absoluto que si contamos con + 1 hacia la derecha, y si contamos hacia la derecha partiendo de un punto cualquiera del campo negativo, invadiremos el positivo, de modo que contar en un sentido con -1 es lo mismo que contar en sentido opuesto con + 1, es decir: a + (-b) = a - b , a - (-b) = a + b. Esta es, sencillamente, la traducción matemática de la regla de los antiguos indios: "Una deuda, restada de cero, enriquece, y una persona es tanto más rica cuantas menos deudas tenga". |
||||||||||
| adición de números racionales |
Véase adición de números naturales, de números negativos y de fracciones ordinarias |
||||||||||
| adición de números reales |
Llamamos suma de dos números reales
p y e:
de la definición resulta que es:
Para que la definición sea válida, hay que demostrar que satisface el principio de las leyes formales. Dado los números reales
supongamos que están definidos por otras dos cortaduras
En virtud del criterio de igualdad y desigualdad, es:
de donde
luego las cortaduras (ai + bi , ai ' + b') , (ci + di , ci ' + di ') definen el mismo número real, lo que demuestra la ley uniforme de la suma; y de una manera análoga se demuestran las demás leyes.
|
||||||||||
| adición de números transfinitos |
Llamamos suma de los números ordinales transfinitos m y n al número que corresponde al conjunto que resulta de colocar los objetos de un conjunto N cuyo tipo de orden sea n a continuación de los de un conjunto M cuyo tipo de orden sea m , conservando el orden de los elementos de ambos conjuntos. Esta restricción es fundamental, pues aplicando por ejemplo, la definición a los conjuntos M = a, de tipo 1 y N = b1 , b2 , b3 ... de tipo w , se tiene: M + N = a, b1 , b2 , ... , bn , ... N + M = b1 , b2 , b3 , ... , bn , ... , a Y es M+N ¹ N+M puesto que para obtener el tipo 1+ w tenemos que formar un conjunto de un solo elemento a y un conjunto del tipo w, v. gr.: una sucesión indefinida b1, b2 , ... , ordenada según los índices consecutivos y considerar en la suma de ambos conjuntos el elemento a como de rango inferior a todos los términos de la sucesión bi , (i = 1,2, ...), en la que subsiste el orden primitivo, resultando el conjunto ordenado a < b1 < b2 < b3 < b4 < ... < bn ... , que es también del tipo w, mientras que para el tipo w + 1 se obtiene el conjunto ordenado < b1 < b2 < b3 b4 < ...< bn < ... < a , cuyo tipo de orden es distinto de w porque tiene un último elemento, de modo que es
Lo mismo se demostraría n + w = w , m + v ¹ v + m ; luego: La suma de números ordinales transfinitos no es conmutativa. Desde el punto de vista cardinal parece, sin embargo, que debe ser À0 + 1 = 1+ À0 ; pero la conmutatividad desaparece en cuanto los dos términos pertenecen a distintos modos de existencia. Puesto que 1 pertenece a À0 , tiene que ser À0 + 1= À igualdad cuyo primer miembro indica que consideramos el elemento perteneciente al conjunto como interviniendo en la constitución de éste y el signo + no indica, por tanto, ningún aumento numérico. De igual modo, la expresión À0 + n se debe interpretar como un número complejo de dos componentes heterogéneos: el conjunto de todos los números naturales y el elemento constitutivo o unidad numérica de este conjunto, y, por tanto, es À0 + n = À0 . |
||||||||||
| adición de polinomios |
Se llama suma de polinomios la expresión que resulta al reunir los monomios que forman los polinomios sumandos, previa reducción de los semejantes. Es práctico escribir los polinomios sumandos, de manera que los monomios semejantes queden en columna. Por ejemplo: (7a + 4bc-4a2) + (-7a - bc + 2b2c) + (5a2 -3bc) 7a + 4bc - 4a2 - 7a - bc + 2b2c - 3bc + 5a2 _______________________ + a2 +2b2c El valor numérico del polinomio suma es la suma de los valores numéricos de los polinomios sumandos, para todo sistema de valores atribuidos a sus letras. |
||||||||||
| adición de potencias de números naturales |
Las propiedades del triángulo aritmético permiten encontrar fórmulas que dan las suma de las potencias de los n primeros números naturales, y así: I. de la identidad i2 = i + i (i-1) , se deduce:
puesto que es
y simplificando:
II. De la identidad
resulta:
y en virtud del triángulo aritmético:
y simplificando:
III. De las fórmulas [1] y [2] sale inmediatamente esta notable igualdad:
que nos dice que la suma de los cubos de los n primeros números naturales es igual al cuadrado de la suma de los mismos. |
||||||||||
| adición de segmentos rectilíneos |
Llamamos suma de varios segmentos consecutivos al segmento que tiene por origen al origen del primero y por extremo, al extremo del último de los segmentos a sumar. Si los segmentos sumandos no son consecutivos, se realiza un transporte adecuado sobre una semirrecta. |
||||||||||
| adición de series |
Si las series
|
||||||||||
| adición de vectores |
La suma de dos vectores OA y OB es la diagonal OS del paralelogramo que determinan. La simple inspección de la figura
demuestra que la parte
Esta regla permite descomponer un vector OS, situados en el plano de dos vectores no colineales OA y OB, en dos componentes paralelos a éstos, para lo cual basta construir el paralelogramo de lados paralelos a OA y OB. La suma OA + OB representa una traslación del plano sobre sí mismo. |
||||||||||
| adición de vectores axiales |
Suma de dos vectores de distintas bases, que se cortan en un punto, es la diagonal del paralelogramo construido con ellos a lo largo de sus bases hasta su punto de intersección. Si las bases son paralelas esta definición no es válida, y entonces llamamos suma de los dos vectores al vector paralelo cuyo momento es la suma de los momentos de los sumandos. Si éstos son más de dos, la suma se obtiene sumando los dos primeros; el resultado se suma al tercero, y, así siguiendo, se llega a un último vector cuyo momento es la suma de los momentos de los sumandos. |
||||||||||
| adigualdad |
Nombre que dio Viète a la igualdad aproximada que empleó en su Methodus ad disquirendam maximam et minimam . Una vez planteada la ecuación de una curva, supone que, en ella, la cantidad A aumenta en otra cierta cantidad, que representa por e, y forma la expresión A + e, que iguala a A, y, luego de reducir la nueva ecuación, anula la cantidad e para obtener la expresión de A que da el máximo o el mínimo que busca. La noción fermatiana de adigualdad fue depurada por Leibniz cuando, prescindiendo no solo de los infinitésimos respecto de las magnitudes finitas, sino admitiendo infinitésimos de infinitésimos o infinitésimos de segundo orden, despreciables respecto de los de primera, consideró de igualdad como un caso particular de la desigualdad diciendo que "la desigualdad infinitamente pequeña deviene una igualdad", lo que le permitió escribir
que hace posible concebir una diferencia
que no resulta de una sustracción en el sentido aritmético de la palabra, sino que corresponde a lo que con frase feliz llamó Milhaud en el Congreso Matemático de Roma, 1900, "el momento infinitesimal de todo devenir". |
||||||||||
| aditiva, función |
Una función f con valores reales y definida sobre un anillo de conjuntos es aditiva si para todo par (P,Q) de elementos disjuntos del anillo se cumple que f(P ÈQ) = f(P)+f(Q). |
||||||||||
| aditivo, monoide | |||||||||||
| adjunción | |||||||||||
| adjunto |
Dada una Matriz A de elementos [aij ], llamamos ( Aij) Adjunto de aij , al valor del determinante cuyo valor se obtiene de multiplicar : (-1) i+j .( Menor Complementario del elemento aij) |
||||||||||
| adjunta, matriz |
Sea M una matriz de m filas y n columnas cuyos elementos son números complejos. La adjunta de M, notada por M* es la matriz conjugada de la transpuesta de M (o la transpuesta de la conjugada que viene a ser lo mismo). |
||||||||||
| adyacente |
Inmediato. Próximo. Elemento geométrico unido a otro bajo ciertas condiciones. |
||||||||||
| adyacentes, ángulos | |||||||||||
| adyacentes, sucesiones |
Una pareja de sucesiones de números reales ((an),(bn)) es adyacente si una de ellas es creciente y la otra decreciente y su diferencia tiende a cero (es decir, ambas son convergentes y tienen el mismo límite). |
||||||||||
| afijo |
Sea P un plano afín asociado al espacio vectorial E y con un sistema de referencia cartesiano (0,B), donde B es una base ortonormal de E. La aplicación que asocia a cada punto P del plano afín con coordenadas (x,y) el número complejo z = x+iy es una biyección de P sobre C. El complejo z es el afijo del punto P. Véase número complejo |
||||||||||
| afín, aplicación |
Sean E y F dos espacios vectoriales sobre el mismo cuerpo K y sean A y B espacios afines asociados respectivamente a E y F. Una aplicación f de A en B es una aplicación afín si existe una aplicación lineal l de E en F, tal que para todo par de puntos (P,Q)Î A2 se cumple l(P). l(Q) = l(P Q). |
||||||||||
| afín, espacio |
Sea E un espacio vectorial sobre un cuerpo conmutativo K. Un conjunto no vacío A es un espacio afín asociado a E si existe una aplicaciónf de A×A en E tal que
|
||||||||||
| afín, geometría |
Estudio de los espacios afines y las variaciones lineales afines junto con los invariantes por el grupo afín. |
||||||||||
| afín, grupo |
Los automorfismos de un espacio afín A forman un subgrupo del grupo de permutaciones de A llamado grupo afín de A. |
||||||||||
| afín, sistema de referencia |
Sea A un espacio afín asociado al espacio vectorial E. Un sistema de referencia afín es toda familia (Mi)i ÎI de puntos de A libres en sentido afín y además generador. |
||||||||||
|
afín,
variedad lineal |
|||||||||||
| afinidad |
Estudio particular de las figuras afines. Relación entre las mismas. En toda afinidad se verifica: I. Las rectas que unen cada par de puntos correspondientes son paralelas porque son rayos proyectantes.
II. Los puntos de intersección de cada par de rectas correspondientes están en una recta que se llama eje de afinidad. III.
La afinidad no cambia cuando el plano de una de las figuras F gira alrededor
del eje de afinidad, pues si
y en virtud del giro se verifica: PA = PA'' , PB = PB'' , y es
luego es A"A' = B"B' , y por la propiedad I, cada una de las figuras es proyección paralela de la otra. IV. Esta propiedad subsiste cuando al girar el plano llegue a quedar abatido sobre el p y, por tanto: La proyección paralela de una figura plana es afín con su abatimiento sobre el plano de proyección, lo que nos permite decir: Dos figuras coplanarias son afines cuando a cada punto y a cada recta de una corresponde un punto y una recta de la otra; las rectas que unen pares de puntos correspondientes son paralelas, y los pares de rectas correspondientes se cortan en puntos que están en línea recta, de modo que para construir la figura afín de una figura F situada en el mismo plano que ésta, se toman en el plano una recta cualquiera r como eje de afinidad y dos puntos cualesquiera A y A' como correspondientes, puesto que así queda fijado el punto P' correspondiente a un punto dado P, y como la recta AA' da la dirección de los rayos proyectantes, para hallar P' basta prolongar PA y por el punto O de intersección con r, trazar OA'. El punto de intersección de esta recta con la paralela AA' por P es la solución. V. La razón de las áreas de las figuras correspondientes es constante, porque considerando, para fijar las ideas, los paralelogramos ABCD y EFGH en un plano, si prolongamos sus lados hasta formar el paralelogramo IJKL, se tiene:
Si
A', B', ..., L' son los puntos homólogos de los A, B, ... , L en el
plano
A'B'C'D', E'F'G'H', I'J'K'L' son paralelogramos en los que se tiene:
y como en los segmentos homólogos AB y A'B', EF Y E'F' se verifica
resulta finalmente:
Si
los planos correspondientes
|
||||||||||
| afinidad homológica | |||||||||||
| afinidad perspectiva | |||||||||||
| afinor | |||||||||||
| a fortiori | |||||||||||
| Agnesi, María Gaetana |
Nació en el año 1718 en Milán, de cuya Universidad fue profesora, cargo que dejó para hacerse hermana de la caridad. Murió en 1799 dejando una obra: Instituzioni analitiche, Milán, 1748, que gozó de un crédito excesivo, y su nombre va unido al de la curva versiera que Grandi le atribuyó. |
||||||||||
| Agostinelli, Cataldo |
Nació en Ceglie Messapica, Italia, en el año 1894. Ingeniero del Politécnico de Turín, fue profesor de Mecánica del Instituto industrial Omar de Novara y después de la misma disciplina en las Universidades de Mesina, Catania y Módena y actualmente de la de Turín. Ha publicado numerosas memorias sobre movimiento de los sistemas rígidos, homografía vectorial, ecuaciones diferenciales, etc. |
||||||||||
| agregado | |||||||||||
| agregar | |||||||||||
| Aguillon, F. |
Jesuita belga, nacido en Bruselas en el año 1556; vivió algún tiempo en España y fue profesor de la Universidad de Amberes, donde murió en 1617. Se dedicó especialmente a óptica, ciencia de la que publicó un tratado, Amberes, 1613, en el que se encuentran sus trabajos sobre proyecciones, y a él se debe la denominación de proyección estereográfica a la de una esfera sobre un plano. |
||||||||||
| aguja de Buffon | |||||||||||
| Ahmes |
Egipcio de hacia el año 1660 antes de J.C., que copió, tomándolo de un escrito muy anterior, el famoso papiro de Rhind, que es el documento más antiguo que se conoce de Matemática. En en British Museum hay dos fragmentos, y otro en la New York Historical society, que llena las lagunas de los de londres, de manera que puede estudiarse en su totalidad. Lenormand fue el primero que dio cuenta de él en los Comptes rendus de la academia de Ciencias de París, 1867; poco después Eisenlohr publicó el texto y la traducción, Leipzig, 1877; posteriormente Peet, Londres, 1923, hizo una edición de lujo, precedida de un estudio en el que rectifica algunos errores cometidos por aquél, y actualmente contamos con una edición facsimilar, acompañada del texto y comentarios hecha por Chace, Bull, Manning y archibald, Oberlin, Ohio, 1927-1929. Ver papiro de Rhind. |
||||||||||
| Aiken, Howard H. |
Norteamericano contemporáneo, nacido en 1900, bajo cuya dirección se construyó la máquina de calcular Mark, en Harvard, el año 1942. |
||||||||||
| Airy, George Bidell |
Astrónomo inglés (1801-1892) que contribuyó a propagar en su país la notación continental del Cálculo infinitesimal, demostrando la superioridad de ésta sobre la newtoniana. |
||||||||||
| aislado, punto |
Sea A una parte de un espacio topológico E. Un punto x Î A es aislado si es posible encontrar al menos un entorno dex que no tenga más puntos de P que el propio x. |
||||||||||
| ajedrez |
Juego entre dos personas, con treinta y dos piezas movibles, sobre un tablero de sesenta y cuatro escaques. La leyenda atribuye su invención a un persa para distraer los ocios de su soberano, quién ofreció a aquél la recompensa que quisiera y él pidió un grano de trigo para el primer escaque, dos para el segundo, cuatro para el tercero y así sucesivamente siempre duplicando el número hasta el sexagésimocuarto escaque, resultando que, al hacer la cuenta, no había bastante trigo en el reino para satisfacer la petición del inventor del juego. Como se ve, se trata de encontrar la suma de la progres |
||||||||||
| alabeado | |||||||||||
| alabeada, curva |
Curva de un espacio afín tridimensional no contenida en ningún plano afín. |
||||||||||
| Albatenio |
Mohámed Abengábir Abenisam Abuadala, conocido vulgarmente por Albatenio, el de Batán, Mesopotamia, nació el a4o 858 y murió en 929. Tuvo la feliz idea de sustituir en sus cálculos la cuerda del arco, que utilizaban los griegos, por la semicuerda del arco doble, es decir, por el seno, y consiguió establecer la fórmula fundamental de la Trigonometría esférica: cos a = cos b. cos c + sen b . sen c. cos A, que demostró después rigurosamente Chéber Benaflah; corrigió las tablas astronómicas de Ptolomeo y en su obra De scientis stellarum, publicada con este título en Nurenberg, 1573, con notas de Regiomontano, está el germien del concepto de tangente trigonométrica, que precisó después Abulguafa. Sus obras completas fueron traducidas al latín por Platón de Tívoli y de las astronómicas hay una edición con texto árabe y latino debida a Nallino, Milán, 1899-1907. |
||||||||||
| Alberto de Sajonia |
Es uno de los más profundos pensadores de la Edad Media (1320?-1390). Formuló claramente la diferencia entre el infinito potencial y el actual y llegó al concepto de límite accesible o inaccesible. |
||||||||||
| Albiruni |
Abualrayán Mohámed, de origen persa (973-1048), llamado Albiruni, escribió sobre una multitud de asuntos científicos, entre ellos los matemáticos, que incluyó en su obra Sobre el cielo y las estrellas, en la que hay varios notables problemas de tercer grado y construcción de polígonos regulares. al ocuparse del eneágono, llega a la ecuación x3 = 1 + 3x, siendo x = 2 cos 20 º, y aunque no dice cómo la resuelve, da la solución x = 1,52I 45II 47III 13IV en el sistema sexagesimal, que tiene, en el decimal, seis cifras exactas. Suter ha hecho una traducción, con comentarios: Das Buch der Auffindung der Sehnen im Kreise, publicada en la Bibliotheca mathematica de Eneström, 1910. |
||||||||||
| Alcarjí |
El algebrista persa Abubéquer Mohámed Abenalhasán, conocido por Alcarjí -calculador de Karkh-, es el más importante matemático árabe del siglo X aunque murió en el año 1029, es decir, a principios del siglo XI. Estudió las ecuaciones
bicuadradas; calculó las raíces aproximadas tomando el valor
siendo r < 2a + 1; ideó la prueba del 9 para la suma y el producto, e introdujo en la Matemática musulmana el Análisis Indeterminado de Diofanto mejorando su simbolismo. Su Álgebra, Al-Fskhri -que está traducida al alemán por A. Hochheim: Kafi fil Hisab des Abu Bekr Mohammed ben Alhusein Alkarchi, Halle, 1879-1880-, influyó en Leonardo de Pisa, como ha demostrado Bortolotti: Le fonti arabe di Leonardo Pisano, en las Memorias de la Academia de Ciencias de Bolonia, 1921. |
||||||||||
| Alcasadí |
Nureddin Abulhasen Alí Abenmohámed el Coraixí el Bastí, vulgarmente conocido por Alcasadí, es el último matemático importante de la España musulmana. Nació en Baza, y siendo muy joven se trasladó a Granada donde hizo sus estudios con Abenfutut y el Saracostí. Luego de la ritual peregrinación a la Meca y de visitar Tlemecén, Túnez y El Cairo, regresó a Granada, de donde tuvo que huir a causa de la guerra, refugiándose primero en Tlemecén y luego en Túnez, donde murió el año 1486. La obra de Alcasadí es muy copiosa, destacándose en ella un tratado de Aritmética y Álgebra, del que abundan los mss en las bibliotecas europeas. En él se encuentran una notación algebraica que es todo lo completa que puede desearse mientras el Álgebra sea numérica, y consiste esencialmente en designar la incógnita y sus potencias por las inicialmente de sus nombres árabes, superpuestas a los coeficientes numéricos; colocar los dos miembros de la ecuación uno a continuación del otro separándolos por uno de los signos de igualdad; escribir en cada uno primero los términos positivos y después los negativos; indicar las proporciones por el signo \ y servirse con perfecta claridad de la notación de exponentes por medio de la palabra ass, que significa principio, base o fundamento. Su Aritmética está traducida y publicada por Woepcke en las actas de la academia de los Nuovi Lincei, 1859, y posteriormente, en 1892, se hizo una edición árabe litogafiada en Fez. |
||||||||||
| aleatoria, variable |
Una función medible X con valores complejos y definida sobre un espacio probabilístico (W,A,P) se denomina variable aleatoria sobre W. |
||||||||||
| alef |
Nombre de la Primera letra Hebrea, equivalente a A o a Véase À |
||||||||||
| Alembert, criterio de d' |
Regla usada para investigar la convergencia de una serie numérica. Sea (an) una sucesión de números reales estrictamente positivos tal que el cociente [(an+1+1)/(an)] admite límite l cuando n tiende a infinito. Entonces si l < 1 la serie ån = 0¥ an converge y si l > 1 diverge. |
||||||||||
| Alembert, Jean Le Rond d' |
Matemático, filósofo y enciclopedista francés. Nació en París en 1717 y murió en esa misma ciudad en 1783. Siendo todavía un niño, estudio en el Colegio de las Cuatro Naciones y en la escuela Mazarin donde destacó en Matemáticas, Física y Astronomía. Después en la Universidad. Sus trabajos se desarrollaron en estos campos: Cálculo integral, mecánica, derivadas parciales, solución analítica de la precesión de los equinocios. Fué colaborados de Diderot en la Enciclopedia Francesa, cuyo Discurso Preliminar se debe a su pluma, d'Alembert escribió en 1739 a la edad de 22 años, una memoria sobre Cálculo Integral, rectificando mucos errores que circulaban entonces sobre el mismo, de él es el Teorema Fundamental del Algebra, que lleva su nombre ; también un criterio de convergencia de series y la solución del problema de la Cuerda Vibrante que enriqueció la Teoría de Ecuaciones en Derivadas Parciales. Sus Opuscules Mathématiques están publicados en 8 tomos, París, 1761-1780, y el examen crítico de su labor puede verse en los Eloges de Condorcet, Tomo III, París, 1848, y de Bertrand, Tomo II, París, 1902. |
||||||||||
| Alexander, James Wadel |
Norteamericano contemporáneo, nacido en 1899, que se dedicó a Topología, en cuya Teoría de Nudos ha encontrado importantes propiedades.- |
||||||||||
| Alexandroff, Paul |
Geómetra alemán contemporáneo, nacido en 1899. Se dedicó a la Topología, a cerca de la cual tiene publicado un tratado en colaboración con H. Hopf, Berlín, 1935.- |
||||||||||
| Alexandrov, compactificación de | |||||||||||
| Alexandrov, Pavel Sergeievich |
Matemático ruso nacido en Bogorodsk (1896) y muerto en Moscú en 1982. Sus principales trabajos tratan sobre topología algebraica. Se le debe la noción de espacio compacto y también fue el primero que uso el término "núcleo de un homomorfismo". |
||||||||||
| alfa |
Nombre de la Primera letra Griega equivalente a A o a . Véase µ |
||||||||||
| álgebra |
Parte de las matemáticas que tiene por objeto el estudio de las estructuras algebraicas, independientemente de la noción de límite. Es la Ciencia de la Cantidad pura, o sea: independiente de toda cualidad, y por lo tanto se la considera como una generalización de la Aritmética, para lo cual representa a los números por letras en vez de cifras, también se la considera actualmente como la parte de la Matemática que se encarga de estudiar las Ecuaciones y los sistemas de ecuaciones de cualquier orden y tipo.- |
||||||||||
| álgebra abstracta o Moderna | Moderna disciplina matemática constituída axiomáticamente, que es una generalización del análisis algebraico. Desarrollada en la década del 50.- | ||||||||||
| álgebra, estructura de |
Sea K un cuerpo conmutativo. Se llama álgebra sobre K a un espacio vectorial E sobre K en el que se ha definido una ley de composición interna multiplicativa que verifica las siguientes propiedades:
En el caso de que la ley multiplicativa sea asociativa se dice que el álgebra es asociativa (en este caso (E,+, ) es un anillo. Si la ley multiplicativa tiene elemento neutro se dirá que el álgebra es unitaria. Si es conmutativa el álgebra se llama conmutativa. |
||||||||||
| algebraica, clausura |
Extensión de un cuerpo conmutativo que sea algebraica y algebraicamente cerrada. |
||||||||||
| algebraica, curva |
Véase algebraica, hipersuperficie. |
||||||||||
|
algebraica,
ecuación |
Sea K un cuerpo conmutativo. Una ecuación algebraica con coeficientes en K es una ecuación de la forma f(x) = 0, donde f es una función polinomial de K en sí mismo. |
||||||||||
|
algebraica,
extensión |
Una extensión L de un cuerpo conmutativo K se llama algebraica si todos los elementos de L son algebraicos sobre K. |
||||||||||
|
algebraica,
geometría |
Estudio de los conjuntos y variedades algebraicas y los invariantes por el grupo de aplicaciones birracionales. |
||||||||||
| algebraica, hipersuperficie |
Sea A un espacio afín asociado a un espacio vectorial E de dimensión finita sobre un cuerpo conmutativo K. Una hipersuperficie algebraica de A es todo ideal principal no trivial del anillo de las funciones polinómicas sobre A. Cuando la dimensión del espacio es 2 las hipersuperficies algebraicas se denominan curvas algebraicas. |
||||||||||
| algebraica, medida |
Sea r una recta afín real y u un vector no nulo de r. Para todo par (P,Q) de puntos de r, el único número real l que cumple P Q = lu se llama medida algebraica de (P,Q). |
||||||||||
| algebraica, topología |
La topología algebraica es una parte de la topología que tiene por objeto descubrir las propiedades de los espacios topológicos y hallar las condiciones necesarias para que dos espacios topológicos sean homeomorfos. |
||||||||||
| algebraico, conjunto |
Sea K un cuerpo y sea Kn el espacio vectorial de las n-tuplas de elementos de K sobre sí mismo. Una parte de Kn es un conjunto algebraico si está formado por puntos (x1,x2,..., xn) que anulan una familia finita de funciones polinomiales |
||||||||||
| algebraico, elemento |
Un elemento a de un álgebra E asociativa y unitaria sobre un cuerpo K, es algebraico sobre K, si existe al menos un polinomio no nulo con coeficientes de K y tal que dicho polinomio se anula para a. |
||||||||||
| algebraico, entero | |||||||||||
| algebraico, número |
Elemento algebraico del cuerpo C de los números complejos, considerado como álgebra sobre el cuerpo de los racionales Q. |
||||||||||
| algoritmo | |||||||||||
| alternada, aplicación p-lineal |
Una aplicación p-lineal sobre un K-espacio vectorial E se denomina alternada si es nula para toda sucesión de p vectores que contenga dos vectores iguales. |
||||||||||
|
alternada,
serie |
Serie de números reales cuyo término general es tal que existe una alternancia de signos positivo y negativo. |
||||||||||
| altura |
Perpendicular a un lado de un triángulo pasando por el vértice opuesto a ese lado. Las tres alturas de un triángulo concurren en el ortocentro. Dícese también de la perpendicular a una cara de un tetraedro pasando por el vértice opuesto. |
||||||||||
|
ampliada,
recta numérica |
|||||||||||
| anamorfis | Transformación de figuras. Figura aparentemente sin sentido pero que lo adquiere vista bajo un cierto ángulo, o por reflexion o refracción sobre una superficie cilíndrica o cónica.- | ||||||||||
| análisis |
El análisis es la parte de las matemáticas que usa los conceptos de sucesión, serie y función. |
||||||||||
| analítica, función |
Sea K un cuerpo (donde K = R o C y sea n un entero positivo. Sea Kn el espacio vectorial usual sobre el mismo cuerpo K. Una función f definida sobre un abierto U de un espacio normado y completo E y con valores en Kn es analítica si para todo z0 perteneciente a U, se puede desarrollar f como serie entera de (z-z0) siendo convergente en un entorno de z0. |
||||||||||
| analítica, geometría |
Estudio de los conjuntos y las variedades analíticas, así como los invariantes por el grupo de isomorfismos analíticos. Ampliar |
||||||||||
|
analítico,
isomorfismo |
Aplicación biyectiva que es analítica con inversa también analítica. |
||||||||||
|
angular,
función |
Sea f(t) aplicación continua de un intervalo I de R en el cuerpo de los números complejos. Existe una aplicación continua a de I en R tal que f(t) = ei a(t) a(t). Tal aplicación recibe el nombre de función angular asociada a f. Dos funciones angulares asociadas a la misma f difieren en un múltiplo de 2 p. |
||||||||||
|
angular,
sector |
Sean (s1,s2) un par de semirrectas con origen comúnO en un plano euclidiano orientado. Sea a un número estrictamente positivo y sea b la medida principal del ángulo entre las dos semirrectas Ang (s1,s2). La unión de todas las semirrectas de origen O y tales que una medida del ángulo Ang (s1,s2) pertenece al intervalo [0,b] si b³ 0 y al intervalo [0,b+2a] si b < 0 es el sector angular de origen s1 y extremos2. |
||||||||||
| ángulo |
Sea U el grupo multiplicativo de los complejos de módulo unidad. La aplicación f que a todo punto u Î U asocia la semirrecta du = f(u) de origen O que pasa por u es una biyección de U en el conjunto de las semirrectas del plano complejo con origen en O. Si notamos por D al conjunto de tales semirrectas y por D2 al producto cartesiano de este conjunto por sí mismo, la relación binaria en D2 definida por (du,dv) º (du¢¢, dv¢¢) si y sólo si u/v = u'/v' es una relación de equivalencia. Las clases de equivalencia de esta relación son los ángulos definidos por pares de semirrectas o simplemente ángulos. |
||||||||||
|
anguloso,
punto |
Punto de un arco geométrico en donde existen semitangentes pero no tangentes. |
||||||||||
| anillo |
Conjunto no vacío dotado de dos leyes de composición interna. Respecto a la primera, notada aditivamente, es un grupo abeliano, respecto a la segunda, notada multiplicativamente, es un monoide y la multiplicación es distributiva respecto de la adición. Si la multiplicación tiene elemento neutro (uno) se dice que el anillo es unitario. Si la multiplicación es conmutativa se dice que el anillo es abeliano o conmutativo. |
||||||||||
|
antihermitiana,
matriz |
Matriz cuadrada de entradas complejas que es igual a la opuesta de su adjunta. |
||||||||||
| antiimagen |
Véase: aplicación. |
||||||||||
| antimorfismo |
Sean E y F dos magmas y sea f una aplicación de E en F. Se dice que f es un antimorfismo si se trata de un morfismo de E en el magma opuesto a F. La definición es análoga para monoides y grupos. |
||||||||||
| antisimétrica, aplicación |
Sean E y F dos conjuntos y p un entero positivo. Una aplicación de Ep en F es antisimétrica si para toda permutación s de {1,2,...,p} y para toda sucesión (x1,x2, ..., xp) de elementos de Ep se cumple que
donde e(s) es el signo de la permutación. |
||||||||||
|
antisimétrica,
matriz |
|||||||||||
|
antisimétrica,
relación binaria |
Relación binaria R en un conjunto E, tal que para todo par (x,y) perteneciente a E, se cumple que: Si x R y e y R x implican x = y. |
||||||||||
| anulador |
Sea E un módulo sobre el anillo A. El anulador de una parte P Ì E es el conjunto de los elementos a del anillo A que verifican ax = 0 para todo xÎ P. |
||||||||||
| aplicable |
Se dice que una superficie S es aplicable sobre otra superficie T si ambas son regulares de orden 1 y además existe un homeomorfismo f de S sobre T tal que se conservan las longitudes de los arcos trazados sobre S. |
||||||||||
| aplicación |
Una aplicación o función es una terna f = (E,F,G), donde E y F son dos conjuntos no vacíos y G un subconjunto del producto cartesiano E ×F tal que para todo elemento x Î E existe un elemento y sólo uno y Î F tal que (x,y)Î G. El conjunto E recibe el nombre de dominio y el conjunto F el de codominio. El elemento único y correspondiente a x por la aplicación f se llama imagen o transformado por x por f y se nota mediante y = f(x). El conjunto de las imágenes de todos los xÎ E por f se denomina conjunto imagen y es una parte de F (eventualmente puede ser todo F). Sea y Î F, se llama antiimagen o imagen inversa de y a todo xÎ E tal que y = f(x). |
||||||||||
|
Apolonio
de Pérgamo |
Matemático griego (Pérgamo circa 260 a.C., Alejandría, circa 200 a.C.). Su trabajo más conocido es el estudio y clasificación de las cónicas como secciones planas de conos de revolución. A él se le deben los nombres de hipérbola y elipse. Se le puede considerar uno de los fundadores de las Matemáticas.- |
||||||||||
| apotema | |||||||||||
|
apoyo,
recta de |
Sea f una función convexa sobre un intervalo I de R. Se denomina recta de apoyo en un punto P del gráfico G de f a toda recta afín que pasa por P y está situada debajo de G. |
||||||||||
| aproximado, valor |
Sean x un número real y e un número real estrictamente positivo. Se dice que a Î R es un valor aproximado de x si pertenece al intervalo (x-e,x+e). |
||||||||||
| arco conexo |
Véase: conexo. |
||||||||||
| argumento |
Sea z un número complejo no nulo. Su argumento principal Arg z es el único valor real q perteneciente al intervalo ]-p, p] tal que
La clase de restos módulo 2 p del argumento principal Arg z se llama argumento de z y se nota por arg z. |
||||||||||
| arista |
Véase: diedro, cara. |
||||||||||
| aritmética, sucesión |
Una sucesión (an) de elementos de un anillo A es aritmética si es posible encontrar un elemento d Î A tal que an+1+1 = an + d para todo n. El valor d se denomina diferencia. |
||||||||||
|
aritmético-
geométrica, sucesión |
Una sucesión (an) de elementos de un cuerpo conmutativo K es aritmético-geométrica si existe un par de elementos (r,d) de K tales que an+1+1 = r an+ d. |
||||||||||
| armónica, función |
Una función f definida sobre un abierto U de Rn con valores complejos es armónica si es dos veces continuamente diferenciable sobre U y su laplaciana es nula: df = 0. |
||||||||||
| Arquímedes |
Matemático e inventor griego. Nació en Siracusa (en la actual Sicilia) en el 287 a. C. y murió en esa misma ciudad durante el saqueo de las tropas romanas en el 212 a. C. Sus trabajos anticipan muchos descubrimientos de la matemática moderna como el cálculo integral. También es autor de inventos tales como el tornillo sin fin, la polea compuesta, etc. Descubridor del principio de hidrostática que lleva su nombre. |
||||||||||
| Arquímedes, espiral de |
Curva plana que admite la ecuación r = a q en coordenadas polares. |
||||||||||
| arquimediano, grupo |
Un grupo conmutativo aditivo G totalmente ordenado se dice que es arquimediano si para todo elemento estrictamente positivo x Î G y todo elemento a Î G existe un natural n tal que a £ nx. |
||||||||||
| arquimediano, valor absoluto |
Dados un anillo unitario A y su unidad e, se dice que un valor absoluto es arquimediano si el valor absoluto de ne tiende a ¥ cuando n tiende a ¥. |
||||||||||
| arreglo | |||||||||||
| Artín, Emil |
Uno de los más grandes matemáticos de este siglo. Nació en Viena en 1898 y murió en Hamburgo en 1962. Sus principales trabajos versan sobre álgebra conmutativa y teoría de números. |
||||||||||
| artiniano |
Un módulo M es artiniano cuando toda sucesión decreciente de submódulos de M es estacionaria. En el caso de un anillo A diremos que es artiniano si considerado como A-módulo es artiniano. |
||||||||||
| Ascoli, Giulio | |||||||||||
| Ascoli, teorema de |
Sea E un espacio compacto y F un espacio métrico y sea C(E,F) el espacio de las aplicaciones continuas de E en F dotado de la distancia de la convergencia uniforme. Para que una parte H de C(E,F) sea relativamente compacta, es necesario y suficiente que H sea equicontinuo y que para todo punto x Î E el conjunto de las imágenes dex por los elementos de H (los cuales son funciones) sea una parte relativamente compacta de F. |
||||||||||
| asíntota | |||||||||||
| asintótica, dirección |
Sea f un arco parametrizado definido en el intervalo real I y sea t0 un extremo del intervalo no perteneciente a éste. Si ||f(t)|| tiende a ¥ cuando t tiende a t0 y si el cociente [(f(t))/( ||f(t)||)] tiende a un límite u cuando t tiende a ¥ se dice entonces que el arco parametrizado f admite por dirección asintótica la recta {lu}. En el caso de que la distancia de la recta afín de dirección marcada por u y que pasa por f(t) tienda a ¥ se dice que el arco parametrizado admite una rama parabólica en la dirección de u. |
||||||||||
| asociados, elementos |
Dos elementos a y b de una anillo de integridad son asociados si a divide a b y b divide a a. |
||||||||||
| asociativo |
Se dice que una ley de composición interna ^ sobre un conjunto E es asociativa si para todo x,y,z Î E se cumple (x ^y)^z = x ^(y ^z). |
||||||||||
| astroide | |||||||||||
| autoadjunto |
Una forma bilineal o sesquilineal se dice autoadjunta si es igual a su adjunta.- |
||||||||||
| automorfismo |
Sea E un magma, un monoide, un grupo, un anillo, un espacio vectorial o un álgebra. Los isomorfismos de E en sí mismo se denominan automorfismos. Isomorfismo en sí mismo, es decir: correspondencia biuníboca entre los elementos de un grupo que conserva el producto. |
||||||||||
| avo, ava |
Terminación que se añade a los números cardinales para indicar las fracciones de la unidad. Parece ser que su orígen es el sufijo del número ordinal octavo, aplicado por analogía a otros ordinales |
||||||||||
| axioma |
Proposiciones que son puestas en el punto de partida de una teoría sin ser deducidas de otras proposiciones. Proposiciones que se admiten como verdaderas sin requerirse su demostración. Son Principios, al estilo de " DIOS EXISTE" Ejemplo: " POR UN PUNTO DEL PLANO, PASAN INFINITAS RECTAS" |
||||||||||
| axioma de Arquímedes. |
Dados dos números existe siempre un múltiplo del menor que supera al mayor.- |
||||||||||
| axioma de elección |
|
||||||||||
| axioma de libre movilidad | |||||||||||
| axioma de Eudoxio |
|
||||||||||
| axioma de Zermelo | |||||||||||
| axiomas de la magnitud. |
|
||||||||||
| axiomas de Peano | |||||||||||
| axiomática |
Construcción puramente deductiva de la Matemática, por medio de un sistema de axiomas o postulados a lños que no se exigen más que dos condiciones: compatibilidad e independencia, es decir que no tengan contradicciones lógicas internas y que ninguno sea corolario de los demás. |
||||||||||
| axiomatismo | |||||||||||
| azimut de un vector | |||||||||||
| azumbre |
Antigua medida de capacidad, para líquidos, equivalente a 2,016 litros |