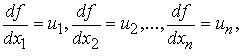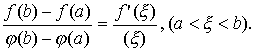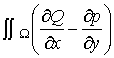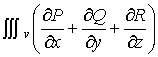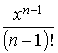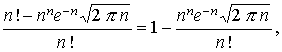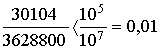| F. | Séptima letra del abecedario de mayúsculas que suele emplearse como característica de las funciones. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f. | Séptima letra del abecedario de minúsculas que se emplea frecuentemente como característica de las funciones. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vigésimaprimera letra del alfabeto de mayúsculas, que Barr
y Schooling emplearon -y han aceptado los tratadistas de Estética- para
representar el valor
de la raíz positiva de la ecuación x2 -x-1 = 0, que es el de la mayor longitud de las dos que se obtienen al dividir un segmento en media y extrema razón. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vigésima primera letra del alfabeto de minúsculas que se emplean como característica de las funciones. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Faà di Bruno, Francesco. | Algebrista italiano (1825-1888), que enseñó en la Universidad de Turín. Se preocupó especialmente de la teoria de funciones elipticas, de la que estaba preparando un tratado completo cuando murió. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Faber, Georg. | Analista aleman contemporaneo, nacido en el año 1877, que se ocupa de la teoria de funciones analiticas. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor. | Cada uno de los términos de un producto. Multiplicador. Divisor. Submúltiplo. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor de Darboux. | Nombre dado por Hermite al valor de
establecida por Darboux. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor de normalización. | Véase producto escalar. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor de proporcionalidad | Constante de proporcionalidad. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor integrante. | El factor por el que hay que multiplicar una expresión diferencil para hacerla integrable. Es fácil demostrar su existencia, pero dificil calcularlo porque hay que resolver una ecuacion en derivadas parciales, y las mas veces cuesta menos integrar directamente la expresion diferencial. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factorial. | Palabra introducida por Arbogast para designar el producto de los n primeros números naturales. Se representa por n! y también por n. Por ejemplo, es 4! = 4 = 1.2.3.4 = 24. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factorizar. | Sacar factor común. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| facultad. | Factorial. Nombre dado por Kramp, que no ha prevalecido. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fagnano, Giulio Carlo conde de. | Analista italiano (1682-1766), que escribió muchos artículos en el Giornale dei Letterati d'Italia sobre Cálculo integral. También se ocupó de la Geometría del triángulo y de la rectificación de curvas, y demostró la interesante propiedad de la lemniscata de poderse dividir, como la circunferencia, 2n , 3.2n , 5.2n partes. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| faja. | Parte del plano comprendida entre dos rectas paralelas, cuya
distancia es la anchura de la faja. Las paralelas son los bordes
de la misma. Este concepto se generaliza al espacio, llamando también faja de anchura a a la parte de espacio comprendida entre dos planos paralelos a distancia a ; pero es mas correcto llamarlo estrato. La posición de una faja queda determinada sin ambiguedad por la de una recta paralela o un plano paralelo a la faja e invariablemente ligada a ligado a ella. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| falsa posición. | Dice Abenersa que la inventaron los indios, pero es lo
cierto que no la conocieron Aryabhata ni Brahmagupta, y solo aparece con
Bhaskara, es decir: un siglo después del sefardí toledano.
Introducida por éste en europa, los españoles e italianos, a partir del siglo XV, abusaron de esta regla -la regula infusa de las Artiméticas del siglo XVII- que ya no se explica en ningún texto porque no sirve para nada. Como curiosidad histórica, diremos que era simple y doble. La simple
se aplicaba para resolver problemas de tipo ax = b, poniendo x =
n, de donde: an = b' y estableciendo la igualdad x : n = b :
b' de la que se deduce el valor x = bn/b' ; y la dobe
consistía en poner primero x = m en los problemas del tipo f(x)
= h, siendo f(x) una función de primer grado, obteniéndose f(m)
= h' = h + k, y luego x = n, resultando f(n) = h'' = h + j,
y el valor de x es
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| falsedad. | Disconformidad del pensamiento con la realidad. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| familia. | Haz .- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fanega. | Del árabe fánica, saco grande. Antigua medida de capacidad para áridos, que tenía 12 celemines. Su equivalencia métrico decimal es 55,5 litros. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fano, Gino | Geómetra italiano contemporáneo, nacido en 1871, a quien se debe, entre otras contribuciones, una nueva dirección de la Geometría proyectiva, a partir del postulado de que la recta determinada por dos puntos, que expuso en su memoria Sui postulati della Geometriaproiettiva di uno spazio lineare ad un numero qualunque di dimensioni, publicada en el Giornale de Battaglini, 1902. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fantappié, Luigi. | Analista italiano (1901-1956), uno de los principales cultivadores de la teoría de funcionales, que la ha aplicado a la integración de ciertos tipos de ecuaciones en derivadas parciales. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fase. | Véase función periódica. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fatou, Pierre
Joseph Louis |
Analista francés (1878-1929), a quien se deben algunos teoremas sobre las singularidades de las funciones meromorfas. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fergola, Nicola | Geómetra italiano (1753-1824), que intentó imprimir a la Geometría una nueva dirección mediante los que llamó métodos de las inclinaciones generalizadas, de conversión o de transferencia y de transposición y rotación, expuestos en su Arte eurística, esrita en 1870, pero no publicada hasta 1842, cuando ya no tenían ningún interés. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fermat, Pierre | Nació el año 1601; estudió Jurisprudencia en Toulouse, en
donde fue magistrado y murió en 1665. Gran admirador de los griegos,
reconstruyó los Lugares planos de Apolonio y tradujo la Aritmética de
Diofanto. Escribió su Isagoge el mismo año que Descartes su
Geometría, 1637, pero no lo dio a conocer, por lo cual se suele
conceder sólo a éste la gloria de haber crado la Geometría analítica,
aunque en la obra de Fermat están los conceptos fundamentales de las
coordenadas expuestos de una manera más clara y más clara y más
próxima a la actual que en la de Descartes. Fermat es también el
fundador de la teoría de números, que le debe muchos teoremas, entre
ellos el que ha pasado a la Historia con el nombre de "último", el
cual ni se ha podido tadavía demostrar ni se ha comprobado su falsedad.
Las obras de fermat han sido publicadas por P. Tannery y Ch. Henry, bajo
los auspicios del Ministerio de Instrucción Pública de Francia, en
cuatro volúmenes y un suplemento, al cuidado de C. de Waard, París,
1891-1922.
Véase último teorema de Fermat. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fernández Baños, Olegario. | Economista español (1887-1946), primer profesor de Estadística matemática, cátedra creada en el año 1933 en la Universidad de Madrid. Amplió estudios en Zurich, Roma y Bolonia, y todos sus trabajos de investigación se refieren a temas de su especialidad: correlación y ecuación de regresión, números índices, curvas de frecuencia, la c2 de Pearson, etc. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ferrari, Ludovico | Algebrista italiano (1522-1565), a quien se debe la fórmula de la ecuación de cuarto grado. Fue discípulo de Cardano y tuvo parte activa en la disputa entre éste y Tartaglia sobre la prioridad de la fórmula de la ecuación cúbica. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ferro, Scipione dal. | Nació en Bolonia el año 1465, de cuya Universidad fue lector de Aritmética a partir de 1496, y parece que es el primero que resolvió la ecuación cúbica de la forma x3+ px + q = 0, punto que no se ha podido poner en claro. Tomó parte en la disputa entre Cardano y Tartaglia y murió en 1526. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Feuerbach, Karl Wilhelm. | Geómetra alemán, cuya breve vida (1800-1834) le impidió continuar la labor de Mobius, Steiner y Staudt, en cuya dirección escribió una obra en la que estudia metódicamente las propiedades de los triángulos rectilíneos. Su nombre va unido en la historia de la Matemática al de Euler en el estudio de la circunferencia de nueve puntos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fi. | Nombre de la vigésimaprimera letra griega. Equivale a F, f.
Véase
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fibonacci. | Véase Leonardo de Pisa. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ficken, Frederick Arthur. | Geómetra norteamericano contemporáneo, nacido en 1910. Es profesor de la Universidad de Tennessee, y ha publicado varias memorias sobre Geometría diferencial y Análisis Vectorial. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fiedler, Otto Wilhelm | Geómetra alemán (1832-1912), que, al sistematizar los métodos de proyección para representar en el plano las figuras y cuerpos del espacio, echó los cimientos de la Geometría descriptiva proyectiva con su Die darstellende Geometrie, 1858. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura. | Conjunto de puntos, líneas, superficies o cuerpos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura autopolar. | La que coincide con su polar recíproca. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura cóncava. | La formada por puntos tales que el segmento que une dos cualesquiera de ellos no siempre pertenece a la figura. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura convexa. | La formada por puntos tales que el segmento que une dos
cualesquiera de ellos pertenece a la figura.
Esta definición se traduce, en particular, para la circunferencia en la propiedad de no poder tener más de dos puntos comunes con una recta. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura finita. | La que tiene dos puntos tales que el segmento que determinan es mayor que cualquiera otro definido por otro dos puntos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura ilimitada | Aquella cuyos puntos no pertenecen todos al contorno de la figura, como la definida, por ejemplo, por los puntos interiores a un plano. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura infinita. | La que carece de una pareja de puntos tales que el segmento que determinan sea siempre mayor que el definido por otros dos puntos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura limitada. | Aquella cuyos puntos petenecen al contorno de la
figura. Por ejemplo: la figura formada por los puntos de un semiplano,
incluso los de su borde, es limitada, como también lo es la constituída
por todos los puntos de un ángulo, incluso los de su lados.
No debe confundirse la figura limitada con la finita. El círculo, por ejemplo, es una figura finita e ilimitada. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura plana. | La situada en un plano. Se puede considerar como conjunto de puntos o como conjunto de rectas. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura radiada. | La formada por todas las rectas o por todos los planos que pasan por un punto, el cual recibe el nombre de vértice. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figura simétrica. | La que, respecto de un punto P, de una recta r o de un plano , es tal que a cada punto A de ella le corresponde otro punto A', que dista de P, de r o de , lo mismo que A. El punto P, la recta r y el plano se llaman centro, eje y plano de simetría, respectivamente. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| figuras afines |
Dos figuras tales que cada una de ellas es proyección paralela de la otra. Véase afinidad. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras afines homológicas |
Dos figuras coplanarias tales que a cada punto y a cada recta de una de ellas le corresponden un punto y una recta de la otra. Todas las rectas que unen pares de puntos correspondientes son paralelas entre sí y cada dos rectas correspondientes se cortan en puntos en línea recta. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras congruentes |
Dos figuras cuyos elementos todos coinciden superponiendo la una a la otra, o también: Dos figuras congruentes son dos posiciones distintas de una misma figura. Si por un movimiento cualquiera hacemos coincidir los extremos A y B de un segmento rectilíneo AB con los A’ y B’, extremos de otro A’B’, ésta superposición asocia a todo punto P de AB el punto P’ de A’B’ cuya posición ocupa el P al final del movimiento, de modo que el concepto de congruencia, nacido de tal superposición, se puede concebir como una correspondencia tal que a todo punto AB se le puede asignar un punto y uno solo de A’B’ y recíprocamente, pues a cada extremo de uno de los segmentos le corresponde un extremo del otro, y que todo segmento interior a uno de los dados se corresponda con un segmento igual del otro, con lo cual hemos restringido, desde el punto de vital lógico, la noción intuitiva de segmentos iguales, y entonces podemos ya decir: a) Todo segmento es igual a sí mismo b) Si un segmento es igual a otro, éste es igual al primero c) Dos segmentos iguales a un tercero, son iguales entre sí d) Un segmento no puede ser igual a ninguna de sus partes Estas propiedades nos permiten transportar segmentos y ordenarlos u orientarlos, y de ellos se deduce la inversión del segmento. Mediante un simple cambio de palabras se establecen las mismas condiciones para los ángulos. Análogamente se define la correspondencia entre los puntos de dos planos, y fijado el concepto de traslación, se establece: 1) Todos los planos son iguales entre sí 2) Todas las rectas son iguales entre sí 3) Se puede construir un segmento ordenado y uno solo igual a otro dado que tenga su origen en un punto de la recta. 4) Todos los ángulos llanos son iguales 5) Dados dos segmentos o dos ángulos a y b, entre ellos existe una de estas relaciones: Ab; a > b; a < b que se completan y se excluyen mutuamente. 6) Existen Segmentos o ángulos mayores y menores que un segmento o ángulo dado. 7) La suma de segmentos y de ángulos goza de las propiedades uniforme, conmutativa, asociativa y de monotonía. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras correlativas |
Aquellas cuyas respectivas definiciones se deducen una de otra combinando la palabra
Así, pues, son correlativas el n-gono
En particular, el triángulo es figura correlativa de sí misma. Si se trata de figuras espaciales, el intercambio de frases es el mismo, pero el de palabras es
y además hay que conservar la palabra recta. Son correlativos el cubo y el octaedro, el dodecaedro y el icosaedro, etc. El tetraedro es correlativo de sí mismo. De la definición de figuras correlativas resulta que a una figura formada por puntos y rectas de un plano, corresponderá otra forma por planos y rectas que pasen por un punto, y por tanto las figuras de primera, segunda, tercera y cuarta categorías, se pueden aparear de esta forma:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras de cuarta categoría |
El espacio como conjunto de rectas. Tiene ¥4 elementos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras de igual
forma |
Figuras semejantes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras de primera
categoría |
La serie rectilínea, el haz de rectas y el haz de planos. Todas tienen ¥ 1 elementos y se puede pasar de una a otra mediante un número finito de proyecciones o de secciones. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras de segunda
categoría |
Las planas y las radiadas. Tienen ¥2 elementos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras
equicompuestas |
Las descomponibles en igual número de partes ordenadamente congruentes sin ninguna parte común, excepto algunos puntos de su contorno. Dos figuras equicompuestas son equivalentes y las equicompuestas respecto de una tercera, son equicompuestas entre sí. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras equivalentes |
Las que tienen la misma extensión. Dos figuras son equivalentes cuando son congruentes o se pueden obtener como sumas o diferencias de figuras congruentes. Véase postulados de
equivalencia. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras homeomorfas |
Aquella entre las cuales se puede establecer una correspondencia biunívoca y continua. Son pues, equivalentes desde el punto de vista topológico. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras homográficas |
Son dos figuras F y F’ ( planas o radiadas) entre las cuales hay una correspondencia tal que a un ( punto o plano) de F corresponde un ( punto o plano) de F’ y a los (puntos de una serie rectilínea o planos que pasan por una recta) de F corresponden los (puntos de una serie rectilínea o planos que pasan por una recta) de F’. Una figura plana se dice homografica de una radiada cuando a un punto y a una recta de la primera corresponden una recta y un plano de la segunda, de modo que si aquel punto está en la recta, su recta homóloga está en el plano homólogo de dicha recta.- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras homológicas |
Las de primera categoría cuando se corresponden punto a
punto y recta a recta , de tal modo que dos rectas homólogas cualesquiera se
cortan en una recta fija y dos puntos homólogos cualesquiera están alineados
con un punto fijo. Las de segunda categoría son homológicas las de especies
distintas cuando sus elementos homólogos son incidentes; las de la misma
especie y bases distintas, cuando sus elementos homólogos son incidentes con
los de una figura de la misma especie, y las superpuestas cuando lo son con una
de la misma especie. Las plantas tienen centro y ejes de homología y las
radiadas, plano central y eje, lo mismo que las de tercera categoría, las
cuales son homológicas cuando entre ellas hay una correspondencia tal que los
puntos homólogos están en rectas de una radiación y los planos homólogos se
cortan en rectas de un plano, de donde resulta que las rectas homólogas están
en planos de aquella radiación y se cortan en puntos de éste plano.
Poncelet, fundó su teoría de figuras homológicas partiendo de un cuadrilátero ABCD y proyectándolo sobre un plano de modo que en la nueva figura, los lados AB, y CD, AD y BC tengan por homólogos pares de rectas paralelas, quedando así transformado el cuadrilátero en un paralelogramo. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras homotéticas |
Dos figuras tales que a cada punto de una de ellas le corresponde un punto en la otra de tal manera que la razón de sus distancias a un punto fijo es constante. Este punto fijo se llama centro de homotecia y la razón constante es la razón de homotecia. Si esta es (positiva o negativa), la homotecia es (directa o inversa). De ésta definición resulta inmediatamente: I- El centro de homotecia es su propio homotético y el único punto que goza de esta propiedad, excepto en el caso de la homotecia directa, y la razón de homotecia es la unidad, pues entonces todo punto coincide con su homotético. II- La simetría central es un caso particular de la homotecia inversa. III- La homotecia inversa cambia el sentido de las figuras Las propiedades fundamentales de las figuras homotéticas son: 1) Dos figuras homotéticas de una tercera respecto del mismo centro y cuyas razones de homotecia tengan el mismo valor absoluto y distinto signo, son simétricas, pues si P’ y P’’ son dos puntos homotéticos de un mismo punto P y están en una misma recta, se verifica, llamando k a la razón de homotecia:
2) Dos figuras F’ y F’’ homotéticas de una tercera F respecto de dos centros O’ y O’’ y de igual razón k, son congruentes, pues los puntos P’ y P’’ homotéticos de P son tales que es:
P’P’’ = O’P(1-k) ., Deduciéndose, pues, una de otra, por una traslación de ambas figuras congruentes. 3) La figura homotética de una recta es una recta paralela a ella, porque si el centro O de homotecia está en la recta, y si O no está en la recta, la homotética de esta se deduce de ella mediante una traslación. 4) La figura homotética de un ángulo, es un ángulo congruente con él, porque tomando como centro de homotecia el vértice del ángulo, si la hotecia es directa, el ángulo es su propio homotético, y si es inversa es el opuesto por el vértice. 5) La figura homotética es un triangulo semejante a él 6) El segmento que une dos puntos A’ y B’ homoteticos de otros dos A y B, es paralelo al segmento Ab y la razón A’B’: AB es igual a la razón de homotecia. Estas propiedades subsisten en el espacio donde además: 7) La figura homotética de un plano es un plano paralelo a él, porque considerando en el plano dado una recta r que gire alrrededor de un punto P, la homotética de r, en cada una de sus posiciones es su paralela que pasa por el punto P’ homotetico de P 8) Un diedro tiene por homotetico un diedro congruente con el 9) Una recta y un plano perpendiculares tienen por homotéticos una recta y un plano perpendiculares. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras iguales |
Véase Figuras congruentes. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras
inversas |
Véase inversión | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Dos figuras tales que los lados de cada una de ellas son líneas isóclinas respecto de los lados de la otra |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras isótopas |
Las homeomorfas que se pueden deformar una en otra | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras perspectivas |
Dos figuras tales que cada una es proyección central de la otra. Las rectas que unen cada para de puntos homólogos pasan por un punto que se llama centro de perspectividad o centro perspectivo, y los puntos de intersección de cada par de rectas homólogas están en una recta que es el eje perspectivo o eje de perspectividad Son perspectivas: a) Una serie rectilínea y un haz de rectas o un haz de planos, cuando cada punto de la serie peretenece al rayo correspondiente del haz b) Un haz de rectas y otro de planos, cuando cada rayo de aquel pertenece al correspondiente de éste c) Dos series rectilíneas de bases distintas, cuando son secciones de un mismo haz de rectas d) Dos haces de rectas de vértices distintos, cuando son perspectivas de una misma serie rectilínea o secciones de un mismo haz de planos. e) Dos haces de planos de aristas distintas, cuando son perspectivas de un mismo haz de rectas f) Dos series rectilínes de la misma base cuando son secciones de dos haces de rectas perspectivos entre sí g) Dos haces de rectas del mismo vértice cuando proyectan dos series rectilíneas perspectivas entre sí o cuando son secciones de dos hacesde planos perspectivos entre sí h) Dos haces de planos de la misma arista, cuando proyectan dos haces de rectas perspectivos entre sí. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras polares recíprocas |
Véase polaridad recíproca |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras proyectivas |
Poncelet llamó proyectivas a las figuras de primera categoría relacionadas mediante un nuevo finito de proyecciones y secciones, definición que después hizo suya Cremona en sus Elementi di Geometría proiettiva, Turin, 1873, para las de segunda categoría, de modo que si son a y a’ dos planos proyectivos, a un punto de a le corresponde un punto de a’ y a los puntos de una recta de a le corresponden los puntos de una recta de a’ y por consiguiente a una recta de a le corresponde una recta de a’ y si un punto de a pertenece a una recta de a, el punto homólogo de a’ pertenece a la recta homóloga. Ahora bien, la polaridad en la circunferencia y el principio de dualidad demuestran que hay otras correspondencias en las que los elementos homólogos son punto y recta , lo cual obliga a modificar la definición anterior diciendo: Que dos planos son proyectivos cuando a un elemento de uno - punto o recta - corresponde un elemento del otro, y a los elementos de una figura de primera categoría de uno corresponden los elementos de una figura de primera categoría del otro. Análogamente esta definición sirve para la proyectividad entre dos haces o entre un plano y una radiación. Esta definición tiene sin embargo, el inconveniente de que no basta para demostrar que en dos planos proyectivos, dos figuras de primera categoría homólogas son proyectivas, y por lo tanto ha habido necesidad de volver a modificarla. Si suponemos para fijar las ideas, que r y r’ son dos series rectilíneas proyectivas en el sentido de Poncelet, r y r’ están relacionadas mediante un número finito de proyecciones y secciones y por lo tanto si A, B, C, D, son cuatro puntos de r y A’, B’, C’, D’ sus homólogos de r’, se tiene: ( ABCD) = (A’B’C’D’), igualdad que podía tomarse como definición de la proyectividad si no exigiera que las bases de las series sean propias; pero como una cuaterna armónica de puntos, de rectas y de planos se puede definir graficamente en todo los casos, Staudt adoptó la siguiente defionición: Dos figuras de primera categría se llaman proyectivas si están relacionadas de modo que a toda cuaterna armónica de elementos de una figura, correponde una cuaterna armónica de elemntos de la otra. O más brevemente: -La proyectividad entre dos figuras de primera categoría es una correspondencia biunívoca que conserva las cuaternas armónicas. -Las de segunda categoría son proyectivas cuando a un elemento de una figura F corresponde un elemento de la otra F’ y a los elementos de una figura de primera categoría de F le corresponden los elemntos de una figura de primera categoría de F’. -La proyectividad entre las figuras de tercera categoría se establece con la condición de que a un elemento del espacio y a los elementos de una figura de segunda categoría le correspondan los elementos de una figura de segunda categría y por último la proyectividad entre figuras de cuarta categía exige ciertas restricciones porque no se puede establecer una proyectividad en el espacio de rectas apoyandose en el concepto de correspondencia biunívoca. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
figuras semejantes: |
Aquellas que se pueden someter a un movimiento que las haga homotéticas. De aquí se deduce que la semejanza es un caso particular de la Homotecia y recíprocamnente, puesto que el movimento de una figura semejante a ( hotettica de ) otra , determina una figura homotética de ( semejante a ) ella, de modo que dos figuras son semejantes ( homoteticas) cuando una de ellas es congruente con una homotetica de ( semnmejante a la otra). La definicion anterir equivale a esta otra: Dos figuras F y F’ son semejantes si entre susu puntos existe una correspomndencia biunívoca tal que la razon de las distancia s entre dos puntos de F a la de los puntos homólogos de F’ es constante para todas las posiciones de los pares correspondientes, y por lo tanrto las distancia s entre los pares de puntos de F y de F’ forman un conjunto de cantidades proporcionales. La razón de las distancias correspondientes se llama razón de semejanza . Si esta es positiva ( negativa) la semejanza es directa ( inversa) . Las figuras semejantes satisfacen las propiedades identica ( reflexiva) Recíproca ( simétrica ) y transitiva, y dos figuras semejantes cuya razón de semejanza sea la unidad, son congruientes . De la definición se deduce tambien que dos figuras semejantes pueden llenar todo el espacio, resultando entonces una correspobndencia biunívoca entre los puntos del espacio, cada uno de los cuakles se puede conciderar como perteneciente a la primera( segunad) figura y tiene un hmólogo en la segunda ( priemera) . Una semejanza transforrma un segmento en otro segmento, una recta en otra recta, un plano en otro plano, dos planos perpendiculares en otros dos plaanos que conservan la perpendicularidad y un diedro en otro diedro,etc. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fila | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fincke, Thomas | Físico suizo( 1561 - 1636), en cuya obra Geometría Rotundi, Basilea, ( 1583) se encuentran por primera vez empleadas las palabras secante y cosecante y la fórmula | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Finé, Oronce |
Astrónomo francés, ( 1494 - 1555) que promovió los estudios de Matemática muy abandonados en su época en Francia, escribió una obra titulada Protomathesis, París ( 1532) en la que expone los elementos de la aritmética, de la geometría y la Cosmografía, comentó ,los elementos de Euclides; Se contaminó con los cuadradores del círculo e hizo una nueva edición de la famosa Margarita Philosophica de Reisch. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Finetti, Bruno de |
Italiano contemporáneo que sostiene el punto de vista del subjetivismo absoluto para fundamentar la probabilidad y la estadística. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Finsler, Paul |
Alemán contemporáneo nacido en 1894. Se preocupa de la Axiomatización de la Matemática, y en la Teoría de Números ha demostrado que el número de primos entre n y 2n crece infinitamente, siendo mayor que n/(3. Log 2n) y menor que 7n/ ( 5. Log n). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fiore, Antonio María |
Italiano de la primera mitad del siglo xvi , discípulo de Ferro, quien le enseño a resolver la ecuación cúbica, lo cual le movió a desafiar a Tartaglia, proponiendole varios problemas que dependían de tales ecuaciones y aceptar, a su vez, de Tartaglia otro desafío análogo. Fiore no resolvió ninguno de los problemas y Tartaglia los resolvió todos. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fisher, Ernest | Austríaco contemporáneo, nacido en 1875, que descubrió al mismo tiempo que Riez, en el año 1907, la correlación que existe entre los dos espacios del Hilbert: el espacio funcional cuyo cuadrado es integrable y el espacio de infinitas dimensiones cuyos puntos son suceciones de números tales que la serie de cuadrados es convergente y por tanto, toda sucesión de cuadrados sumable determina una función de cuadrado integrable en el sentido de Lebesge. La correspondencia entre ambos espacios es Biunívoca y como además se corresponden la suma y la diferencia, los dos espacios son isomorfos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fisicalismo: |
Palabras acuñada por Otto Neurath para designar la doctrina del Circulo de Viena, que propugna la enunciación de las cuestiones cintíficas en el lenguaje de la Física. El fisicalismo es pués una sintáxis del Idioma de la Ciencia que excluye toda combinación de palabras sin sentido. Es decir: Todo pseudo problema lo mismo en las ciencias Naturales que en las del Espíritu, englobándolas todas en la Einheitswissaenschaft: Ciencia Unitaria cuya rama matemática considera tautológica. Primero contra Kant, que afirmaba el carácter sintético |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Flauti, Vicenzo. |
Geómetra italiano (1782-18763), con cuyo Trattato di Ceometria descrittiva Nápoles, 1800, dio a conocer en su patria la creación de Monge, especialmente en Nápoles, en donde hubo una verdadera escuela de geómetras, cuyos trabajos aparecieron en los Opuscoli matematici fundados por Flauti en 1811. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fluente. | Véase fluxión. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| flujo de un vector. |
Producto de un área s por la proyección del vector sobre la normal a la misma. Este es el llamado flujo elemental por ser el s un elemento de área. El flujo total a través de un área S es el límite de la suma de todos los flujos elementales, o sea la integral doble.
que, si la superficie es cerrada, representa el volúmen por unidad de tiempo que queda en la superficie, es decir: la diferencia entre el flujo que entra y el que sale. La significación física del flujo de un vector depende de la magnitud que represente el vector; y asi por ejemplo si es la velocidad de un fluído, el flujo es el caudal que pasa por s; si es una radiación luminosa, eléctrica, calorífica, etc. el flujo es la cantidad de energía s en la unidad de tiempo, etc. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fluxión |
Nombre que dió Newton a la velocidad del movimiento que engendra la fluente; y al palntearse el problema de determinar la fluente partiendo de la fluxión, llegó al concepto de derivada como fluxión de la fluente respecto de la variable. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| focal | Perteneciente o relativo al foco. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| foco | Véase elipse, hipérbola y parábola. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| folio de Descartes. |
Función Cúbica definida por la ecuación x3
+ y3 - 3axy=0
Es la curva más sencilla que tiene un
unicursal y admite una asíntota cuya ecuación
es y = - (x+a). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Foix-Candole, François. |
Obispo francés (1502-1594), cuyos conocimientos matemáticos utilizó el papa Gregorio XIII en su bula Inter gravissimos, de 24 de febrero de 1582, que contenía los elemntos de la reforma del calendario. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fontaine
des Bertins, Alexis. |
Nació en el Delfinado hacia 1705 y murió en Cuisseaux en el año 1771.
Fue un autodidacta que en 1765 se deshizo de su biblioteca para evitar la
posibilidad de plagiar, absurdo criterio que lo condujo a topar con teroremas
que ya estaban descuvbirto.
Perdió mucho tiempo en buscar un método general para resolver una ecuación de cualquier grado descomponiendo su primer miembro en factores por medio de tablas adecuadas. Otro problema que le preocupó fue el de la integración de ecuaciones diferenciales, y aunque no encontró el método general que buscaba , contribuyóal progreso de la teoría demostrando que la integral general de la ecuación de n - simo grado tiene n constantes arbitrarias. Sus escritos están publicados con el título Mémoires de Mathématique, París, 1764. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fontenelle Bernard le Bovier de. |
Erudito francés (1657-1757) cuyos Elogios académicos han legado a la ciencia 69 biografías de sabios que son preciosos documentos para el estudio de la época. Escribió unos Entretiens sur la pluralité des mondes, enderezado a las damas, que tuvieron gran éxito y unos Elements de Géometrie de l’infini, París, 1727, que fueron un perfecto modelo de razonamientos imperfectos. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| forma. |
En Geometría, figura; en Análisis, invariante. El objeto de la teoría de formas es el estudio de las variaciones que sufren cuando entre las variables se hace una sustitución. Suponiendo, para fijar las ideas, tres variables, si hacemos la sustitución el determinate de los coeficientes l,m,n es el módulo de la transformación, la cual se llama unimodular cuando el módulo es 1. Representando por u1 , u2, ... , un las derivadas de la forma j de las variables x1, x2 , ... , xn que contienen y considerando la sustitución
se obtiene una nueva forma Y (u1 , u2 , ... , un) equivalente a la primera. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
forma adjunta a
otra. |
La equivalente a ella cuando el módulo de la transformación es distinto de cero. Si representamos por u1 , u2, ... , un las derivadas de una forma f relativa a las variables x1 , x2 , ... , xn que contiene y consideramos la transformación
Se obtiene una nueva forma F(u1 , u2 , ... , un) Equivalente a la f si el módulo no es nulo, que es la adjunta a ella. Geométricamente: si f = 0 representa una cónica es coordenadas puntuales, F = 0 es la ecuación tangencial de la misma cónica. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| forma algebraica. |
Polinomio homogéneo respecto de las variables que contiene. La forma se llama binaria, ternaria, cuaternaria, etc., según que contenga dos, tres, cuatro, etc., variables y es lineal, cuadrática, cúbica o bicuadrática si es de primero, segundo, tercero o cuarto orden. En particular, una forma es bilineal cuando es lineal respecto de dos series de variables consideradas separadamente, biternaria si contiene dos series de tres variables, etc. Supongamos, para fijar las ideas, una forma ternaria de cualquier orden. Esta forma, igualad a cero, representa en coordenadas homogéneas una curva que, en general, carece de puntos dobles, de modo que para que tenga uno es necesario que sus coeficientes cumplan una cierta relación, es decir: la condición de existencia de tal punto vendrá dada por una cierta función de los coeficientes f(a, b, c, ...) = 0. Si cambiamos de ejes, y son a’, b’, c’ ... , los nuevos valores de los coeficientes, la función anterior se convierte en f(a’ , b’ , c’, ... ) = 0. Ahora bien, es claro que tal propiedad subsiste independientemente de la posición de los ejes; luego las dos funciones anteriores se deben anular simultáneamente para todos los cambios posibles, de ejes, para lo cual es necesario y suficiente que sólo difieran en un factor numérico o en una potencia del módulo de la sustitución. Las funciones de los coeficientes que tienen la propiedad de conservar elo mismo valor, salvo una potencia del módulo de la sustitución lineal cualquiera son invariantes de la forma dada. El número de invariantes distintos de una o varias formas es finito porque, expresando para cada uno de ellos la propiedad de invariación, se obtiene una serie de ecuaciones que sólo contienen el determinante de la sustitución y si el número de estas ecuaciones excede de un cierto número se podrá eliminar el detreminante de la sustitución y los nuevos coeficientes primitivos: resultado absurdo. En particular, el número de invariantes de una forma única es igual, a lo más, al número de relaciones que pueden existir entre los coeficientes de esta forma y los de su transformada aumentado en una unidad. En las formas binarias se verifica el teorema de hermite: El número de invariantes de orden n con respecto a los coeficientes de una forma binaria de orden p, es igual al número de invariantes de orden p de una forma de orden n. Si la forma binaria es de orden impar 2n - 1, se puede reducir de una manera única a una suma de n términos seguida de un término adicional. En las cuadráticas, cuyo estudio reviste especial interés por sus aplicaciones a los problemas de máximos y mínimos, teoría de números, curvas y superficies de segundo grado, etc., se demuestran que si contienen n variables se pueden reducir de infinitos modos a una suma algebraica de n cuadrados independientes. La teoría de las formas puede estudiarse en A. Capelli: Lezioni sulla teoria delle forme algebriche, Nápoles, 1902. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Forma algebraica
equivalente a otra. |
La que se deduce de ella mediante una transformación unimodular. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Forma canónica. |
La que no se puede simplificar más sin restringir su generalidad mediante sustituciones lineales. Si x, y, z, u, representan formas lineales que son, según los casos, dependientes o independientes, las formas x2 + y2 ................... binaria x2 + y2 + z2 ............ ternaria ax2
+ by2 + cz2 + du2 cuaternaria x3 + y3 .................... cúbica binaria x3 + y3 + z3 + 6axyz cúbica ternaria x3 + y3 + z3 + u3 ...... cúbica cuaternaria x4 + y3 + 6ax2y2 ...... bicuadrática binaria por ejemplo, son formas canónicas. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
forma cuadrática. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| forma diferencial cuadrática. |
La
establecida por Riemann para caracterizar cada espacio, por medio de la
distancia entre dos puntos infinitamente próximos, que, en el fondo, es una
generalización del teorema de Pitágoras:
ds2 = åaij
dxidxj ,
(i = j = 1, 2, 3, ... , n). Si se verifica, en particular ds2 = dx12 + dx22 + ... + dxn2 el espacio es euclídeo o de curvatura nula. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
forma exponencial de
un número complejo. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
forma normal. |
Forma canónica. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
formalismo . |
Orientación de la Matemática que tiende a construir esta ciencia axiomáticamente. Véase axiomática. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
formas
indeterminadas. |
Véase límite indeterminado. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula. |
Resultado de un cálculo cuya expresión, reducida a sus términos más sencillos posibles, sirve de regla para resolver todos los casos análogos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fórmula de Ampère. | Véase Fórmula de Stokes. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Cardano.
|
Véase ecuación cúbica. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Cauchy. |
Dadas dos funciones f (x) y j (x) derivables en el intervalo (a, b), cuyas derivadas no se anulan en ningún punto del intervalo, y es f (b) ¹ f(a) y j (b) ¹ j (a), se verifica:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Frénet-Serret. |
Llamando a, b, c ; a’, b’, c’ ; a’’, b’’, c’’ a los cosenos directores de la tangente, de la normal principal y de la binormal a una curva alabeada, se tiene: Que permiten calcular los radios de curvatura R1 y R2 de flexión y de torsión cuando se conocen los nueve cosenos directores. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fórmula de Green. |
Si es W un recinto simplemente conexo de contorno C, y P y Q dos funciones continuas y uniformes de x é y, se tiene:
La primera de estas dos fórmulas: fórmula de Green en el plano, permite transformar una integral doble en curvilínea y viceversa, y la segunda: fórmula de Green en el espacio, permite transformar una integral triple en una superficie y viceversa. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fórmula de Herón. |
Para calcular la superficie de un tríángulo S =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Mac Laurin. |
Es la de Taylor para h = 0, resultando: F(x)
= f (0) +
Esta fórmula supone que f(n-1) (x) es continua en el intervalo (0, x) y que f(n) (x) está definida en el mismo intervalo. Al desarrollo tayloriano se puede aplicar el de Maclaurin siempre que de origen a una serie convergente, es decir: el desarrollo en serie de Maclaurin es válido para los valores de x que hagan que el término complementario tienda a cero cuando n crece indefinidamente. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fórmula de De Moivre. |
Véase potencia de un vector y potencias de base compleja y exponente entero. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Newton |
Vése potencia de un binomio. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fórmula de Simpson. |
Se emplea para calcular el área aproximada de un recinto limitado por una curva, el eje OX y dos ordenadas extremas correspondientes a las abscisas a y b. Dividiendo el recinto por ordenadas equidistantes, llamando h a la distancia entre ellas, E a la suma de las extremas, I a la de las impares y P a la de las pares, la fórmula de simpson es:
S =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de
Stirling. |
Para encontrar valores aproximados de las factoriales de números muy grandes que se presentan en los problemas de probabilidades, se emplea la siguiente fórmula dada por Stirling;
N! = nn e-n
El error absoluto que se comete tomando este valor de n! crece con n, pero el relativo es
que puede hacerse tan pequeño como queramos dando a n valores muy grandes, y así, por ejemplo, para n = 10, la férmula da 3598696 y como el verdadero valor es 10! = 3628800, pero el relativo es
y podemos, por tanto, contar con dos cifras exactas. Para n = 100, la fórmula da 9324847.10157 y por ser exactamente 100! = 93326215.10157, el error relativo es menor que el 0,08 %; para n = 1000, la fórmula da 40235.102563 , que tiene cuatro cifras exactas, etc. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Stokes. |
Representando por ....? una curva cerrada trazada en una superficie en la cual determina un recinto G, Stokes demostró que es Fórmula que permite transformar una integral de superficie en curvilínea y viceversa. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Taylor. |
Dada una función racional y entera de una sola variable F(x) = a0xn +a1xn-1+... + an-1x+an, si ponemos x + h en vez de x, se tiene: f(x+h) = = a0
(x+h)n + a1(x + h)n-1 + ... + an-1
(x+h) + an. Desarrollano los paréntesis del segundo miembro por la fórmula del binomio, derivando la fórmula dada y aplicando el mismo proceso a las derivadas sucesivas, resulta la siguiente fórmula debida a Taylor: Que sólo es válida cuando f(x) es un polinomio; pero se generaliza para una función cualquiera en un intervalo (a , b) si admite derivadas sucesivas finitas en el punto a, siempre que en vez del último término complementario conveniente, resultando así: Este término Rn tiene diversas expresiones, entre ellas, las siguientes: Debidas a Schlömilch, Lagrange y Cauchy, respectivamente. La fórmula de Taylor tiene excepcional importancia, pues si el término complementario o resto tiende a cero cuando n ® a , se puede prolongar indefinidamente, y al ser entonces lím Rn = 0, resulta la expresión de f(b) en serie convergente. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula de Wallis. |
La que da el
valor de
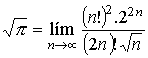
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fórmula del
binomio. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| fórmula de los incrementos finitos. |
Si x1 es la abscisa del punto de contacto de una tangente a una curva definida por la ecuación Y = f(x) = 0 , la fórmula de los incrementos finitos es
de la que se deduce inmediatamente: I. La derivada de una constante es nula y recíprocamente. II.
III. Si una función es creciente / decreciente en un intervalo, su derivada es positiva / negativa o nula en este intervalo. Véase teorema del valor medio, teorema de la media y variación de las funciones. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Forsyth,
Andrew Russell. |
Analista inglés contemporáneo (1858-1942), que ha hecho notables aportaciones a la teoría de funciones. Son muy importantes sus dos obras Theory of differential equations en cuatro volúmenespublicados por la universidad de Camgridge, 1906, y Theory of functions of two complex variables, Cambridge, 1914. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fourier, Joseph. | Nació en Auxerre, Francia, en el año 1768, cuyo obispo lo protegió al quedar huérfano siendo muy niño, internándolo en la Escuela Militar que regentaban los benedictinos. En 1789 marchó a París y tomó parte en las revueltas callejeras de la Revolución, y en el mismo año presentó a la Academia de Ciencias una memoria que le valió ser nombrado alumno de la Escuela normal, donde conoció a Monge, con quien estuvo en Egipto acompañando a Napoleón durante su campaña de 1798; en 1808 fue nombrado prefecto del Isere con residencia en Grenoble donde redactó su Teoría analítica del calor que presentó a la Academia en el año 1807, obra que introdujo en el Análisis las series trigonométricas, llamadas de Fourier |